此问题即可以在非耦合表象中求解，也可以在耦合表象中做，并且，所得到的结果应该是完全一样的。
首先，选用非耦合表象。用
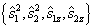的共同本征函数作为基底，即
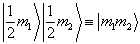（5）
由于， 
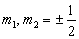，所以，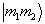 
只有四种组合方式，将其按如下顺序编号：
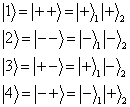（6）
它们满足正交归一化关系
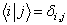（7）
显然，在所选的基底之下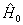 
是对角矩阵，通过简单的计算可以得到其对角矩阵元为
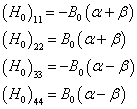（8）
对于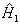 
而言，计算中需要用到升降算符的计算公式
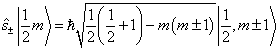（9）
计算结果为
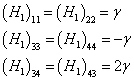（10）
其余的矩阵元皆为零。最后，得到哈密顿算符在非耦合表象中的矩阵形式
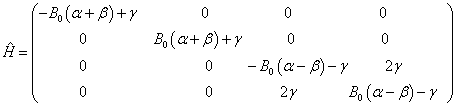（11）
这是一个准对角的矩阵，它的头两个本征解可以直接写出来，即
，
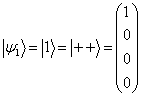（12）
，
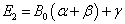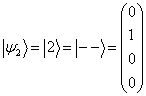（13）
另外两个解需要在剩余子空间中求出。若令
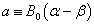（14）
则久期方程为
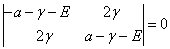（15）
将其整理成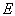 
的一元二次方程
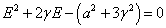（16）
此方程的解为
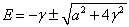（17）
再令
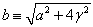（18）
则另外两个本征值分别为
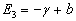（19）
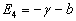（20）
当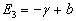 
时，将其代回剩余子空间中的本征方程
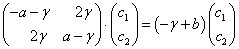（21）
于是得到
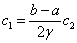（22）
利用归一化条件得到
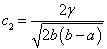（23）
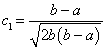（24）
于是，求出了第三个本征值对应的本征矢