例题7.7
设电子在均匀磁场 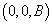 中运动,其哈密顿算符为
中运动,其哈密顿算符为
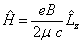 ,
,
试建立
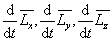
所满足的运动方程,进而解出
 ,
,
已知,当 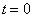 时,
时,
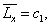
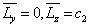 。
。
解:由定义知
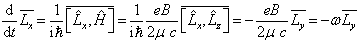 (1)
(1)
式中,
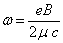 (2)
(2)
同理可知,
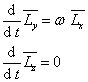 (3)
(3)
由
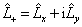 知,
知, 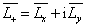 ,进而得到
,进而得到
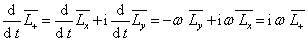 (4)
(4)
此即算符 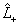 的平均值满足的微分方程。对上式积分,得到
的平均值满足的微分方程。对上式积分,得到
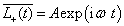 (5)
(5)
于是,有
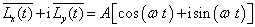 (6)
(6)
比较等式两边可知
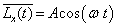 (7)
(7)
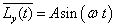 (8)
(8)
而由(3)式知
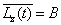 (9)
(9)
最后,利用初始条件定出常数
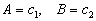 (10)
(10)
将其代入(7)-(9)式,得到
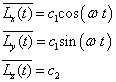 (11)
(11)
例题7.8
两个自旋为 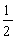 、固有磁矩分别为
、固有磁矩分别为
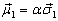
和
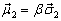
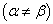
的非全同粒子,处于均匀磁场
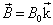 中。若它们之间的相互作用为
中。若它们之间的相互作用为 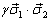 ,求体系的能量本征值和相应的本征矢。其中,
,求体系的能量本征值和相应的本征矢。其中, 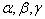 为实常数。
为实常数。
解:由题意可知,可以不顾及空间自由度,体系的哈密顿算符为
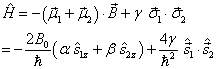 (1)
(1)
为了计算方便,将哈密顿算符写成两部分,即
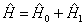 (2)
(2)
式中,
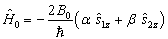 (3)
(3)
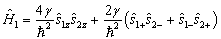 (4)
(4)