例题7.6
若体系是由三个自旋为 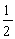 的非全同粒子组成的,且其哈密顿算符为
的非全同粒子组成的,且其哈密顿算符为
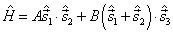
其中, 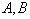 为实常数。试找出体系的守恒量,并求出体系的能级与简并度。
为实常数。试找出体系的守恒量,并求出体系的能级与简并度。
解:将粒子1和粒子2自旋之和记为 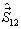 ,三个粒子的总自旋记为
,三个粒子的总自旋记为 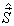 ,即
,即
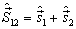 (1)
(1)
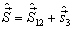 (2)
(2)
显然,
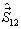 与
与
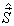 都具有角动量的性质,而三个粒子的角动量之间相互对易,且
都具有角动量的性质,而三个粒子的角动量之间相互对易,且
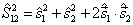 (3)
(3)
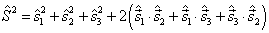 (4)
(4)
哈密顿算符可以改写成
 (5)
(5)
由于,
 (6)
(6)
所以,
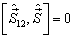 (7)
(7)
进而可知, 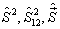 都是守恒量,故可选
都是守恒量,故可选 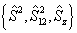 作为力学量的完全集,共同本征函数为
作为力学量的完全集,共同本征函数为 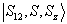 ,其中,各量子数的可能取值为
,其中,各量子数的可能取值为
 (8)
(8)
体系的能量本征值只与量子数
![]() 有关,即
有关,即
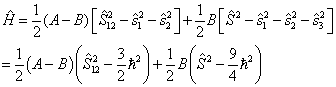 (9)
(9)
具体的能量本征值为:
当 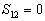 时,
时,
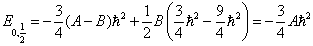 (10)
(10)
其简并度为2。
当 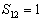 时,
时,
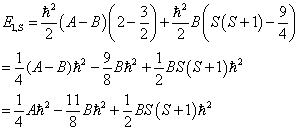 (11)
(11)
若 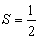 ,则
,则
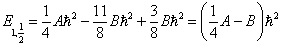 (12)
(12)
其简并度为2。
若  ,则
,则
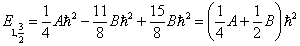 (13)
(13)