习题 7.9
设算符
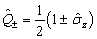
在  表象中写出其矩阵形式,并证明如下关系成立:
表象中写出其矩阵形式,并证明如下关系成立:
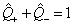 ;
;
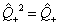 ;
;
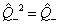 ;
;
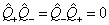
 ;
; 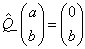
习题 7.10
证明
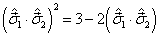
并由此求出 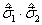 的本征值。
的本征值。
习题7.11
设体系由两个自旋为  的非全同粒子构成,若体系处于两个粒子的自旋状态分别为
的非全同粒子构成,若体系处于两个粒子的自旋状态分别为 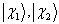 的状态中,分别求出体系处于单态与三重态的几率。其中,
的状态中,分别求出体系处于单态与三重态的几率。其中,
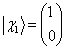 ,
,

习题7.12
设电子在均匀磁场  中运动,
中运动, 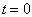 时,处于
时,处于 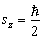 的状态,若将磁场的方向突然转向
的状态,若将磁场的方向突然转向  方向,即
方向,即 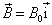 ,求
,求 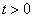 时测得
时测得 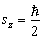 的几率。
的几率。
习题7.13
两个自旋为 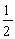 的非全同粒子构成一个复合体系,设两个粒子之间的相互作用为
的非全同粒子构成一个复合体系,设两个粒子之间的相互作用为 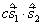 ,其中,
是常数。设
,其中,
是常数。设
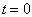 时粒子1的自旋沿
时粒子1的自旋沿 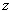 轴正向,粒子2的自旋沿
轴正向,粒子2的自旋沿 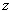 轴负向,求
轴负向,求 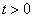 时测量粒子1的自旋处于
时测量粒子1的自旋处于 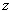 轴正向的几率。
轴正向的几率。
习题 7.14
自旋为 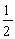 的粒子处于一维阱宽为
的粒子处于一维阱宽为  的无限深势阱中,若其状态为
的无限深势阱中,若其状态为

求其能量的可测值及其相应的取值几率。其中, 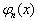 为该无限深势阱的第
为该无限深势阱的第  个本征态。
个本征态。
习题7.15
自旋为
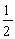 的粒子处于线谐振子位势中,
的粒子处于线谐振子位势中, 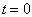 时,粒子处于状态
时,粒子处于状态
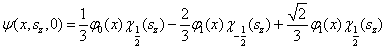
求
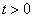 时的波函数,能量的取值几率与平均值。
时的波函数,能量的取值几率与平均值。 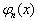 为该线谐振子的第
为该线谐振子的第  个本征态。
个本征态。
习题7.16
设两个电子同处于球谐振子场中,若不顾及电子之间的库仑相互作用,当一个电子处于基态,而另一个电子处于第一激发态时,求两个电子体系的波函数。
习题7.17
设体系由三个全同玻色子构成,且该玻色子只有两个可能的单粒子态 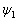 和
和  。若忽略粒子之间的相互作用,问体系可能的状态有几个,它们是如何由单粒子波函数构成的。
。若忽略粒子之间的相互作用,问体系可能的状态有几个,它们是如何由单粒子波函数构成的。