§8.1
无简并微扰论
设
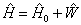 ,已知
,已知
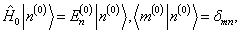 (8.1.1a)
(8.1.1a)
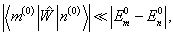 (8.1.1b)
(8.1.1b)
且
 本征矢无简并。求解
本征矢无简并。求解
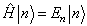 。
(8.1.2)
。
(8.1.2)
由于
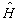 的复杂性,(8.1.2)难于求出准确解。下面求出它的近似解。为了确定近似的精度,将
的复杂性,(8.1.2)难于求出准确解。下面求出它的近似解。为了确定近似的精度,将
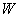 重写为
重写为
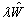 ,相应的
,相应的
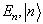 可写为
可写为
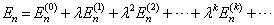 (8.1.3)
(8.1.3)
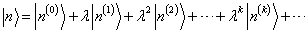 (8.1.4)
(8.1.4)
这里
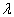 初始看作很小的参数,将近似解按
初始看作很小的参数,将近似解按
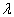 的幂次分开后,再将
的幂次分开后,再将
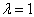 代入。
代入。
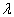 也可以是实际的标志相互作用强度且小于1的常数。将(8.1.3)-(8.1.4)代入(8.1.2),并将其中
也可以是实际的标志相互作用强度且小于1的常数。将(8.1.3)-(8.1.4)代入(8.1.2),并将其中 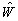 用
用 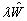 代替,按
代替,按
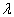 的幂次列出等式,得到各级修正满足的方程
的幂次列出等式,得到各级修正满足的方程
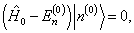 (8.1.5)
(8.1.5)
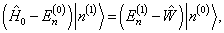 (8.1.6)
(8.1.6)
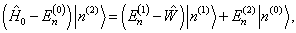 (8.1.7)
(8.1.7)
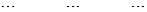
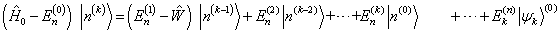
(8.1.8)
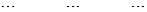
下面依次求解这些方程。零级近似(8.1.5)的解已知,因此首先求解(8.1.6)。
一级微扰
由于
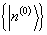 是完备系,可将
是完备系,可将 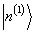 向
向
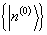 展开,
展开,
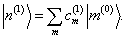 (8.1.9)
(8.1.9)
(8.1.9)代入(8.1.6),得到
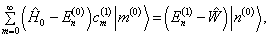
再用
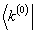 左乘(8.1.6)两边,考虑到
左乘(8.1.6)两边,考虑到
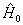 的厄密性(
的厄密性(
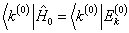 )及
)及 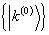 的正交归一性,得到
的正交归一性,得到
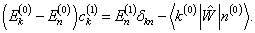
当
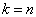 ,得到
,得到
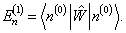 (8.1.11)
(8.1.11)
当
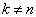 ,得到
,得到
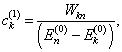
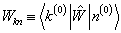 (8.1.12)
(8.1.12)
下面再求 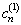 。近似到
。近似到 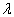 的
的 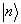 是
是
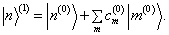
近似到 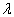 一次幂的
一次幂的
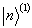 的归一化是
的归一化是
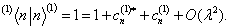 (8.1.13)
(8.1.13)
由此得
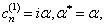 (8.1.14)
(8.1.14)
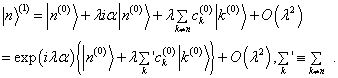 (8.1.15)
(8.1.15)
可见,既是 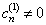 ,它也只是改变
,它也只是改变 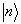 无关紧要的整体相因子。因而,为方便可选择
无关紧要的整体相因子。因而,为方便可选择
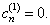 这样,近似到
这样,近似到 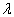 一次幂、归一化的
一次幂、归一化的 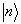 是
是
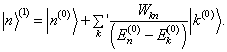 (8.1.16)
(8.1.16)