§9.1.2
弹性散射
1、弹性散射满足的方程
将坐标原点选在A与B的质心处，质心看作是相对静止的。在质心坐标系中，相对运动的定态薛定谔方程为
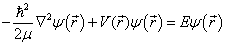（9.1.4）
其中，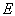 
为入射粒子的能量， 
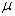为折合质量
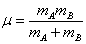（9.1.5）
设势场是中心力场，
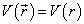（9.1.6）
且令
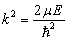（9.1.7）
则（9.1.4）式可写成
（9.1.8）
其中，
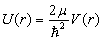（9.1.9）
2、入射波与散射波
散射波的渐进行为。相对于测量散射粒子的距离，
A与B相互作用范围是很小的。所以，只需要考虑 
的情况，这时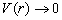 
。方程（9.1.8）的解是球面波
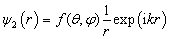（9.1.10）
其中， 
称为散射振幅。由于粒子沿
轴入射，对应的入射平面波为
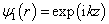（9.1.11）
这相当于单位体积中有一个入射粒子。在
处，入射粒子被散射后的状态为
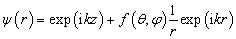（9.1.12）
下面利用上式导出微分散射截面与散射振幅之间的关系。
根据
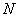与 
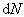的定义知
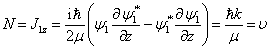（9.1.13）
（9.1.14）
利用微分散射截面的定义可知
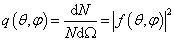（9.1.15）
由（9.1.12）得到这个结果似乎部队，因为求概率时没有考虑（9.1.12）两项交叉项的贡献。实际上可以证明，在远处（
），除了
之外，干涉项可以忽略（量子力学 卷1 曾谨言 科学出版社
1997 第482页）。因此（9.1.15）是正确的。由（9.1.15）可知，只要知道了散射振幅就可以得到微分散射截面，而散射振幅要通过求解（9.1.8）式得到。但是，严格求解方程（9.1.8）是十分困难的，通常要采用近似方法。