§9.2
李普曼-许温格方程
下面在边界条件(9.1.12)下,用Green函数法求解(9.1.8)。按Green函数法的步骤,首先定义满足如下方程的Green函数 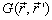 ,
,
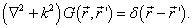 (9.2.1)
(9.2.1)
这个方程的右边及 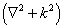 都是平移不变的,因此
都是平移不变的,因此
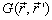 也是平移不变的,
也是平移不变的,
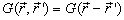 。作傅利叶变换
。作傅利叶变换
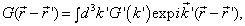 (9.2.2)
(9.2.2)
考虑到
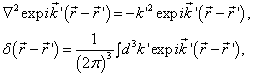
将(9.2.2)代入(9.2.1)可得
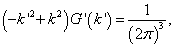
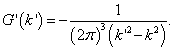 (9.2.3)
(9.2.3)
由(9.2.2)得
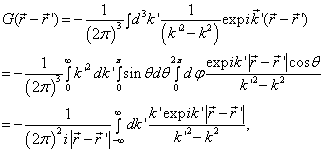 (9.2.4)
(9.2.4)
为计算此积分,将
 延拓到整个复平面。显然,
延拓到整个复平面。显然, 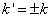 是被积函数的一级极点。可由留数定理算出这一积分。选取不同的回路将有不同的结果。物理要求推迟波,即出射波。考虑到对于出射波,
是被积函数的一级极点。可由留数定理算出这一积分。选取不同的回路将有不同的结果。物理要求推迟波,即出射波。考虑到对于出射波, 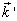 与
与 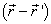 夹角
夹角 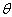 应有
应有 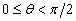 ,
, 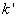 的回路应选为
的回路应选为
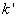 的实轴及在上半平面绕回,如图所示。
的实轴及在上半平面绕回,如图所示。

图9.2 积分回路
当回路取在上半平面时
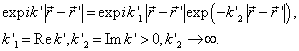
可知沿上半圆的积分为零。由此应用留数定理,有
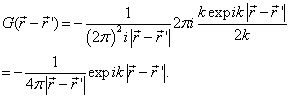 (9.2.5)
(9.2.5)
令
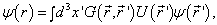 (9.2.6)
(9.2.6)
则 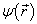 是(9.1.8)的一个解。因为
是(9.1.8)的一个解。因为
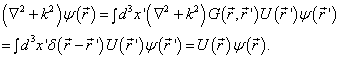 (9.2.7)
(9.2.7)
(9.1.8)的通解是
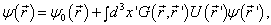 (9.2.8)
(9.2.8)
此即李普曼(Lippmann)-许温格(Schwinger)方程。 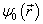 满足相应的齐次方程,
满足相应的齐次方程,
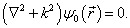 (9.2.9)
(9.2.9)
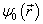 代表未经散射的波,因此取为入射波
代表未经散射的波,因此取为入射波 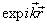 。将(9.2.5)代入(9.2.8)得到
。将(9.2.5)代入(9.2.8)得到
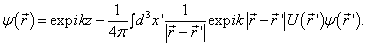 (9.2.10)
(9.2.10)