§9.3
玻恩近似
由(9.2.10)可看出,如果 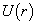 是一个比较光滑寒暑,那么当
是一个比较光滑寒暑,那么当![]() 很大时,振荡因子
很大时,振荡因子 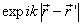 将使积分变小,从而可将
将使积分变小,从而可将
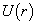 看作微扰。这意味着(9.2.10)适用于高能散射。(9.2.10)被积函数含有所要求解的未知函数,是一个积分方程,这时可用迭代法逐级求解。将(9.2.10)右边
看作微扰。这意味着(9.2.10)适用于高能散射。(9.2.10)被积函数含有所要求解的未知函数,是一个积分方程,这时可用迭代法逐级求解。将(9.2.10)右边  用零级近似代替
用零级近似代替
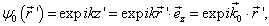 (9.3.1)
(9.3.1)
可得一级散射波函数,称为一级玻恩近似,这里  是
是 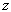 方向基矢,
方向基矢,  是入射粒子的动量,沿
是入射粒子的动量,沿
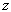 方向。再逐步迭代,可得高级近似。
方向。再逐步迭代,可得高级近似。
如果
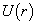 的力程是有限的,则(9.2.10)的积分只限于一个有限范围。当
的力程是有限的,则(9.2.10)的积分只限于一个有限范围。当 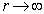 时,
时,
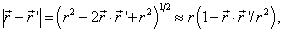 (9.3.
2)
(9.3.
2)
 (9.3.3)
(9.3.3)
 (9.3.4)
(9.3.4)
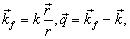
由于是弹性散射,
 。
。
这样,如图图9.3可见,

图9.3
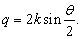 (9.3.5)
(9.3.5)
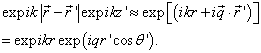 (9.3.6)
(9.3.6)
式中  是
是 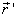 相对于
相对于 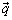 的夹角。设
的夹角。设 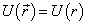 ,将(9.3.
4)和(9.3. 6)代入(9.2.10)可得
,将(9.3.
4)和(9.3. 6)代入(9.2.10)可得
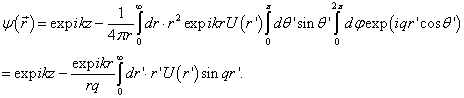 (9.3.7)
(9.3.7)
将(9.1.12)与(9.3.7)比较可得
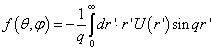 ,
(9.3.8)
,
(9.3.8)

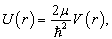
 (9.3.9)
(9.3.9)
玻恩近似成立的条件
由(9.3.
7)可见,当
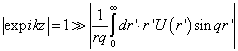 (9.3.10)
(9.3.10)
时,玻恩近似能够是一个好的近似。具体分析如下。
(1)
如果入射粒子能量很低, 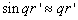 , 设
, 设 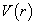 的力程
的力程 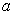 ,大小
,大小 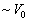 ,(9.3.10)化为
,(9.3.10)化为
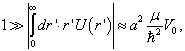 或
或
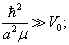
(2)
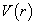 的力程
的力程
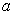 很小。这时(9.2.20)化为
很小。这时(9.2.20)化为
 或
或
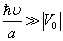 ;
;
(3)
入射粒子能量足够高。这时被积函数由于相因子的快速振荡而相消,积分值将变得很小。这样,如果玻恩近似在低能区成立,则在高能区也成立,但反过来,却不一定。