§9.4
分波法
分波法是处理散射问题的一个严格方法。但由于实际上不可能计算全部分波,所以也是一种近似方法。这种方法适合于低能散射。
本节势场都是中心力场。
§9.4.1
散射振幅和相移
1.入射平面波按球面波分解
入射粒子显然用 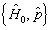 的共同本征态, 即平面波·
的共同本征态, 即平面波·
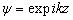 (9.4.1)
(9.4.1)
描述更方便。然而中心力场的问题显然在球坐标系中处理更方便。中心力场的力学量完全集是  。这些量也是守恒量。充分利用这些守恒量对于处理散射问题很重要。
。这些量也是守恒量。充分利用这些守恒量对于处理散射问题很重要。 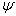 是
是  的共同本征态(
的共同本征态(  ),但不是
),但不是 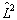 的本征态。为在球坐标中处理散射问题,可将
的本征态。为在球坐标中处理散射问题,可将
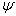 向
向 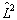 的本征态展开。
的本征态展开。
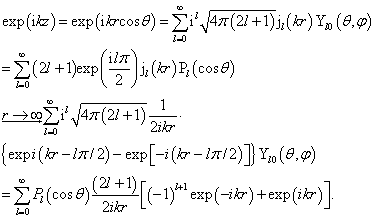 (9.4.2)
(9.4.2)
2.相移和散射截面
假设散射势场是中心势场  。这样,散射是绕
。这样,散射是绕 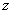 轴对称的,与
轴对称的,与  角无关。相应的薛定锷方程和渐进条件分别是,
角无关。相应的薛定锷方程和渐进条件分别是,
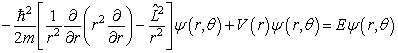 , (9.4.3)
, (9.4.3)
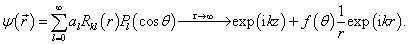 (9.4.4)
(9.4.4)
由于角动量守恒,平面波分解(9.4.2)中的各个不同的 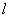 分波将各自独立散射,每一个分波都满足(9.4.3)和渐进条件(9.4.4)。即
分波将各自独立散射,每一个分波都满足(9.4.3)和渐进条件(9.4.4)。即
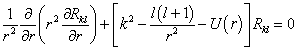 (9.4.5)
(9.4.5)
式中
 ,
, 
为化简(9.4.5),设 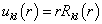 ,(9.4.5)变为
,(9.4.5)变为
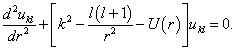 (9.4.6)
(9.4.6)
散射振幅决定于方程(9.4.6)的解。为与渐进条件(9.4.4)比较,考虑(9.4.6)的渐进解。 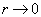 ,由
,由 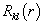 的有限性可知,应有
的有限性可知,应有
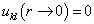 ;
(9.4.7a)
;
(9.4.7a)
 时,(9.4.6)变为
时,(9.4.6)变为
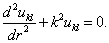 (9.4.7b)
(9.4.7b)
由此得到
 (9.4.8)
(9.4.8)
为了与(9.4.2)相应的项比较,已将待定位相中分出了 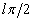 。将(9.4.6)求出解后,确定其渐进形式并与(9.4.8)比较,就确定了重要的位相
。将(9.4.6)求出解后,确定其渐进形式并与(9.4.8)比较,就确定了重要的位相  。
。
将这样确定的
 代入到以下两个公式,就求得了微分散射截面和总散射截面。
代入到以下两个公式,就求得了微分散射截面和总散射截面。
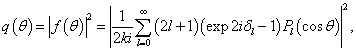 (9.4.9)
(9.4.9)
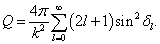 (9.4.10)
(9.4.10)
下面证明这两个公式。