由(9.4.8)可得  ,代入(9.4.4)得
,代入(9.4.4)得
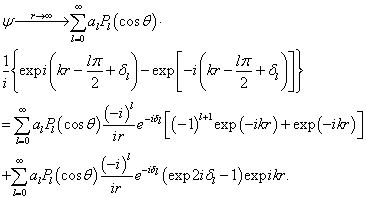 (9.4.11)
(9.4.11)
将(9.4.11)右边第一项与(9.4.2)比较,并考虑到(9.4.4)可得
 (9.4.12)
(9.4.12)
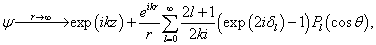 (9.4.13)
(9.4.13)
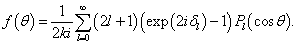 (9.4.14)
(9.4.14)
由  和(9.4.14)得(9.4.9)。考虑到
和(9.4.14)得(9.4.9)。考虑到 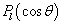 的正交归一关系
的正交归一关系

可得总散射截面
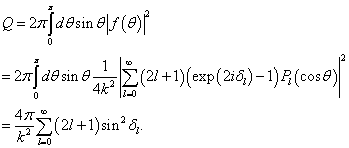 (9.4.15)
(9.4.15)
这样就证明了(9.4.9)和(9.4.10)。
3.讨论
A.
由以上推导可看出,入射波(9.4.2)中的第 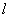 个分波经散射势场作用后,产生相移,由原来的
个分波经散射势场作用后,产生相移,由原来的  变成为
变成为 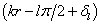 。
。 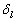 由方程解在
由方程解在 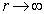 时的渐进形式确定。
时的渐进形式确定。
B.
显然  时,
时, 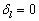 。设无散射的第
。设无散射的第
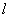 个分波的一个确定位相位为
个分波的一个确定位相位为  时,
时, 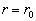 。相应的散射波中第
。相应的散射波中第
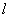 个分波的这个位相为
个分波的这个位相为 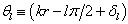 时,如果
时,如果 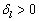 ,则
,则  ,说明
,说明 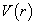 是吸引势,即
是吸引势,即 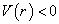 ;如果
;如果  ,则
,则  ,说明
,说明
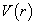 是排斥势,即
是排斥势,即 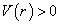 。
。
由(9.4.9)和(9.4.10)可看出,微分散射截面和总散射截面与 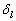 的符号无关。
的符号无关。
C.
分波法的适用条件。实际计算中不可能对无穷多个分波求和。因此分波法也有其适用条件。
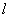 越大,角动量越大,从经典物理看,入射粒子距离散射中心也就越远,受散射中心作用也小。因此,
越大,角动量越大,从经典物理看,入射粒子距离散射中心也就越远,受散射中心作用也小。因此,
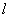 越大,
越大,
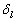 应越小。当
应越小。当  时,就不必考虑比
时,就不必考虑比
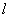 更大的分波了。入射粒子的动量是
更大的分波了。入射粒子的动量是 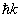 。设
。设
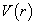 的作用半径为
的作用半径为 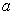 ,则当
,则当 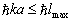 ,即
,即 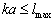 就不必考虑比
就不必考虑比  更大的分波了。由此可见,分波法适于低能或作用半径很小的势场。
更大的分波了。由此可见,分波法适于低能或作用半径很小的势场。
4.光学定理
总截面  正比于弹性散射部分向前散射振幅的虚部,即
正比于弹性散射部分向前散射振幅的虚部,即
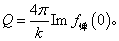 (9.4.16)
(9.4.16)
证明:由(9.4.14)和(9.4.15)可得,
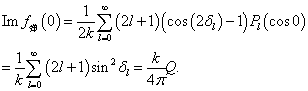
这是一个普适规律。其物理解释是,总散射截面是入射波减弱的量度。而这种减弱是入射波和向前散射波(二者同方向)相消干涉结果。向前散射波振幅越大,消掉的入射波振幅也越大,入射波剩余振幅就越小,因而被散射部分(包括非弹散射和吸收截面)就越大。
5.
例题
设入射粒子被钢球方势垒
 (9.4.17)
(9.4.17)
散射,考虑低能散射,计算其  波的散射截面。
波的散射截面。
解:以 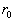 为界,将位势分为两个区域,相应的方程分别为
为界,将位势分为两个区域,相应的方程分别为
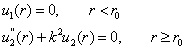 (9.4.18)
(9.4.18)
式中 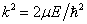 。方程(9.4.18)的解为
。方程(9.4.18)的解为
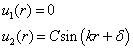 。
(9.4.19)
。
(9.4.19)
利用波函数在 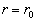 处的连接条件可知
处的连接条件可知
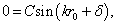
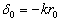 。
(9.4.20)
。
(9.4.20)
于是,散射截面近似为
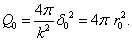 (9.4.21)
(9.4.21)
按经典物理,钢球散射截面显然是  ,这是很直观的。而按量子力学,低能(即长波)散射却是钢球球面。按经典物理,这是不可理解的。而按量子力学,这同样是很直观的。因为伴随低能入射粒子的、波长很长的德布罗意波有很显著的绕射作用,结果钢球完全被入射粒子的德布罗意波包围,粒子可以碰撞到钢球球面的任意点,这样,总散射截面自然就是整个球面了。这一散射清楚地说明了经典力学和量子力学散射的差别。
,这是很直观的。而按量子力学,低能(即长波)散射却是钢球球面。按经典物理,这是不可理解的。而按量子力学,这同样是很直观的。因为伴随低能入射粒子的、波长很长的德布罗意波有很显著的绕射作用,结果钢球完全被入射粒子的德布罗意波包围,粒子可以碰撞到钢球球面的任意点,这样,总散射截面自然就是整个球面了。这一散射清楚地说明了经典力学和量子力学散射的差别。