13．证明：
（1）若一个算符与角动量算符
的两个分量对易，则其必与
的另一个分量对易；
（2）在
与
的共同本征态
下，
与
的平均值为零，且当
时，测量
与
的不确定性之积为最小。
解：（1）设
由角动量对易关系
可得
(2). 由升降算符
及
得，
显然，当
时，
最小。
14．在
表象中，
.
试用微扰论求能量的二级修正。
解：
由此得
因为
，
所以
。
由
得
将上述值代入
即得修正到二阶的能级。
15．质量为
的粒子作一维自由运动，如果粒子处于
的状态
上，求其动量
与动能
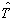的几率分布及平均值。
解：
动量
的几率分布及平均值是
