§4.7
补充材料
2、例题（看懂即可，掌握方法）
下面仅举几个具有使用价值的例子来说明(4.7.6)式的具体应用。
（1）
对于坐标算符，有
(4.7.15)
证明：
由定义知
(4.7.16)
（2）
对于动量算符，证明爱仑弗斯特(Ehrenfest)定理：
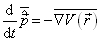(4.7.17)
证明：
(4.7.18)
考虑到，
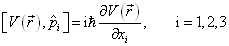(4.7.19)
可得(4.7.17)式。
（3）
证明维里（Virial）定理：
若哈密顿算符为
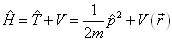(4.7.20)
对于定态而言，则有
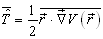(4.7.21)
证明：
因为
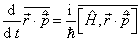(4.7.22)
将(4.7.20)式代入上式，得到
(4.7.23)
其中，
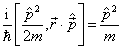(4.7.24)
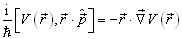(4.7.25)
于是，有
(4.7.26)
对于定态而言，
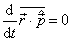(4.7.27)
将其代入(4.7.26)式，可知(4.7.21)式成立。特别是，若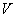 
可以写成
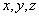的齐次函数形式时，则有
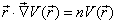(4.7.28)
维里定理可以简化为
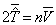(4.7.29)
（4）
证明费曼-海尔曼（Hellmann）定理：
对哈密顿算符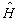 
的束缚定态
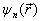而言，有
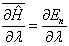(4.7.30)
其中，
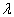是算符
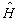中的一个参数，
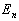是对应
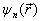的本征能量。
证明：
因为
(4.7.31)
所以，有
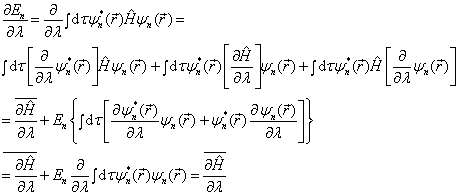(4.7.32)