新 数 学 化 一、"数学化"的含义     人们运用数学的方法观察现实世界，分析研究各种具体的现象，并加以整理组织，以发现其规律，这个过程就是数学化；简单地说，数学地组织现实世界的过程就是数学化。 数学的产生与发展本身就是一个数学化的过程，人们从手指或石块的集合形成数的概念，从测量、绘画形成图形的概念，这是数学化。数学家从具体的置换群与几何变换群抽象出群的一般概念，这也是数学化。     数学的整个体系，作为充满着各种各样内在联系与外部关系的整体结构，它并非是一个僵硬的、静止的骨架，它是在与现实世界的各个领域的密切联系过程中发生、形成并发展起来的。就像线性函数起始于自然和社会中的比例关系，数量积开始于力学，以及导数开始于速度、密度、加速度等，可以这么说，整个数学体系的形成就是数学化的结果。     数学教育应该尊重数学的传统，要按照历史的本来面目，根据数学的发展规律来进行。当儿童通过模仿学会计数时，当他们把两组具体对象的集合放在一起而引出加法规律时，这实质上是历史上现实世界数学化过程的再现。我们当然没有必要也没有可能将数学教学过程变成历史发展过程的机械重复，但确实必须也可以从中获得很好的借鉴。事实证明，只有将数学与它有关的现实世界背景紧密联系在一起，也就是说只有通过"数学化"的途径来进行数学的教与学，才能使学生真正获得充满着关系的、富有生命力的数学知识，使他们不仅理解这些知识，而且能够应用。     因此在为学生准备数学的过程中，我们应该记住弗赖登塔尔的名言：与其说是学习数学，还不如说是学习"数学化"；与其说是学习公理系统，还不如说是学习"公理化"；与其说是学习形式体系，还不如说是学习"形式化"。他特别指出，数学本身同样属于现实世界，因而在数学发展过程中，我们必然要面对数学自身的数学化。     人们在长期的实践中，将朴素直观的各种几何命题加以组织、整理、加工，形成欧几里得公理系统，这一通常称为公理化的过程，实质上也是一种数学化。近年来数学发展的重要特征之一，就是公理化思想广泛地渗入各个领域。例如从置换群与几何变换群形成一般群的公理系统，从实数域与复数域建立起一般域的公理系统等等。我们的数学教学自然不能停留在让学生的头脑成为形形色色公理系统的仓库，更重要的任务是必须教会学生能运用自己的数学思维，对一个数学领域进行加工、整理，从而独立地建立起一个公理体系来。也就是说，必须让学生学会公理化。     如果说公理系统是通过公理化的方法重新组织数学内容的结果，那么作为数学抽象性的特点之一的形式体系就是通过形式化的方法重新组织数学语言的表达，从而建立起来的结构。这种形式体系化，或简称形式化，实质上是另一种数学化。数学内容的特殊本质决定了对数学语言的特殊要求，从日常语言中逐渐独立出来，引进特定的数学术语来表达数学的活动与思想。从希腊人的以字母表点、以文字代数，到阿拉伯人建立的完整的数字符号系统，从而使代数运算及有关的规律形成了完美的体系；17世纪以来，大量新符号的引进，以至近代将逻辑符号引入了数学；所有这些都是数学的形式化过程的逐步提高与发展。随着近年来计算技术的突飞猛进，预计数学的形式化程度还将达到更高的水平，数学科学自然也将随着这个形式化过程而进到一个更高的阶段。数学教学当然不能为形式而形式，只让学生死记硬背那些形式符号与逻辑体系，只作机械的而无内涵、无意义的运算操练。我们必须使学生学会用正确的数学语言来组织并表达数学的现实内容及内在联系，从而构成严谨的体系，也就是必须让学生学会形式化。 二、"数学化"的结构与成分     由于每个人都有自己特有的不同的"数学现实"，因此数学化就有不同的层次与特征，这里借用荷兰有关专著中的框图（见图1.1）来体现有关现实世界与数学化的关系以及它的不同水平的特点这一总体结构。 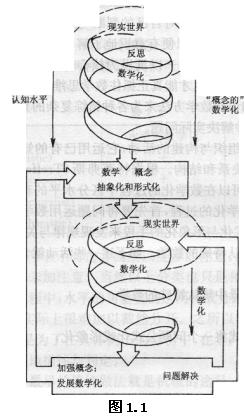    首先，现实世界自始至终贯串在数学化之中，我们常把由现实世界直接形成数学概念的过程称为"概念的"数  学化， 它往往随着不同的认知水平而逐渐得到提高；与此同时，对这个概念的形成过程进行反思，作更为抽象与形式的加工，再用它来解决现实世界的问题，通过现实世界的调节作用，使数学化得到进一步的发展与演化，而由此形成的新的方法手段又能用于组织更高一层的现实世界，并产生新的数学概念。现实世界的数学化就是这样，通过两者交融在一起，经常地相互反馈信息，促使数学现实世界与数学化持续不断地发展与提高，这就是数学科学持续发展的动力，这也同样应该成为数学教育持续发展的动力。     其次，反思是数学化过程中的一种重要活动，它是数学活动的核心和动力。数学的不少发现来自于直觉，而分析直觉、作出表达与解释，从而深入理解、作出判断并确认其推理过程，则是通向数学化的道路。必须让学生学会反思，对自己的判断与经历的活动包括语言表达进行思考并加以证实，以便有意识地了解自身行为后面潜藏的实质，只有这样的数学教学--以反思为核心--才能使学生真正深入到数学化过程之中，也才能真正抓住数学思维的内在实质，从而借助自己的数学知识与数学方法来为各种错综复杂的具体现象构造相应的数学模型，并解决实际问题。     数学化是一种组织与构建的活动，它运用已有的知识与技能去发现未知的规律、关系和结构。根据特莱弗斯（Treffers）和哥弗里（Goffree）的提法，可以在数学化的过程中区分水平的和垂直的两种成分。为了实现数学化的过程，首先要将问题运用数学的方式来陈述，即为了通过图式化与形象化的手段来发现规律与关系，首先必须从一般的背景中确认特殊的数学。如下述一些活动就含有较强的水平成分：       ●从一般的背景中辨认特殊的数学；     ●图式化；     ●以不同的方式将一个问题公式化或形象化；     ●发现关系；     ●发现规律；     ●在不同的问题中识别其同构的本质；     ●将现实世界的问题转化为数学问题；     ●将现实世界的问题转化为已知的数学模型。     当问题一旦转化成或多或少具有数学性质的问题时，我们就可以运用数学工具来着手处理了，也就是现实世界的问题的数学加工与整理，实质上已经转化到数学的范畴了。如下述一些活动就含有较强的垂直成分：     ●将某个关系表示成公式；     ●证明一些规则；     ●调整与完善模型；     ●使用不同的模型；     ●将一些模型汇集并综合在一起；     ●形成新的数学概念；     ●推广并建立起一般化的理论。     借助于数学化的两种成分，我们可以用下列图表来比较四种不同类型的数学化途径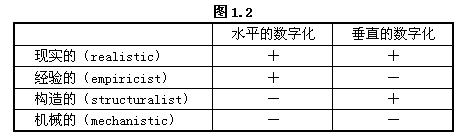：     其中"＋"号表示对这方面给以更多的注意，而"－"号则表示较少注意或根本未加注意。当然以上分类也只是相对比较而言，在实际的数学化过程中，水平的与垂直的这两种成分的作用相互缠绕，关系错综复杂，实际上很难加以截然分开。之所以将其区分为两方面的成分，也只是为了在具体例子的分析中，在不同方法论的辨认中，可以更为清晰地描述与判定。     数学教育最早的传统做法就是机械的途径，教师将各种结论灌输下去，学生被动地接受这些结果，死记硬背，机械模仿，不知道它的来龙去脉，所获得的只是知识的形式堆砌，既不考虑它有什么用处，也不问它们互相之间是否有内在联系，可以说很少包含数学化的思想。以后逐渐有所进步，比较多地考虑到实际的经验，也建立了不少现实的模型，从而进入了经验的途径，即较多地顾及数学化的水平成分，使所获得的数学知识具有一定的实用价值，可以解决一些客观现实中的问题。如有的国家所设置的"消费者数学"之类。但这些知识又往往流于琐碎、零星、不成体系，忽视了数学本身的内在联系，尤其是忽略了数学的逻辑演绎结构，较少注意数学化的纵深发展。为了纠正上述偏向，以布尔巴基观点为代表的"新数学"运动的做法，就采用了构造的途径，强调数学的演绎结构，重视逻辑推理的论证，企图以结构主义的思想来组织整个数学教学，以提高抽象的逻辑思维水平、形成严谨的演绎结构体系作为唯一的目标，从而又由一个极端走向了另一个极端，忽视了数学的现实性，忘却了数学教育的根本目标还是要为现实的社会服务；而且一味追求抽象，强调严谨，也不符合教学规律与学生的认识规律。     总结历史的经验教训，我们应该得出的结论是：数学教育的正确途径应该是现实的数学化途径，我们需要为学生准备的数学课程体系应该全面而完善地体现"数学化"的思想，既要强调现实基础，又要重视逻辑思维，既要密切注意数学的外部关系，也要充分体现数学的内在联系，并且将这些侧面有机地结合在一起；当然最根本的是使学生在直观与抽象的结合过程中，提高数学知识水平，掌握数学技能与方法，并且运用这些数学知识、技能以及思想方法，来观察、比较与识别现实世界中的具体问题，并在类比、归纳的实际经历过程中，建立数学模型，或是找出其共性与规律，形成数学的抽象与概括，也就是学会"数学化",那才是数学教学所必须遵循的正确路线。 三、实现"数学化"过程的数学教学理论     荷兰的范·希尔（van Hiele）夫妇从中学的几何教学实践出发，面对学生在几何学习中表现出来的问题和困难，在理论与实践两个方面进行了探索、实验和总结、提高，概括出了关于几何学习思维水平的理论体系，这对如何通过数学化途径进行数学教学是个很好的借鉴。     他们把几何的思维划分为五个水平     0-水平：直观 其特征是学生借助直观形象，笼统地从外表上接受整体的图形概念，并不理解其构造、关系，也不进行比较。譬如学生知道矩形、正方形、菱形和平行四边形，也会画这些图形，但对它们的认识是孤立而不相联系的，认为这些图形是完全不相关的。     1-水平：分析 其特征是学生开始识别图形的构造和互相之间的关系，也能借助于观察、作图等方法非形式地建立起图形的许多性质，但并未掌握其间的必然联系。譬如学生知道矩形有四个直角、对边相等、对角线相等，但并未深入追问这些性质互相之间是否有什么联系？对这些性质的掌握只限于各种现象的罗列；再如学生完全知道一般的平行四边形和矩形一样也具有对边相等的性质，但却并未想到矩形概念应该从属于平行四边形概念。     2-水平：抽象 其特征是学生形成了抽象的定义，也能建立图形概念与性质之间的逻辑次序，但尚未对演绎的实质含义形成清晰的观念。根据思维变化与对象的不同特点，学生会混合使用实验观察与逻辑推理等各种不同的推导方法，但还没有理解公理的作用，自然更谈不上对数学内在结构体系的掌握。譬如学生知道矩形的定义，也能知道正方形是矩形、也是平行四边形；学生还可以以平行四边形的某个性质为出发点，推出其他的性质；但却还没有掌握整体的逻辑联系，还不知道哪些概念是基本的，而另一些性质却是派生的。     3-水平：演绎 其特征是学生抓住了整个演绎体系，能在以不定义的基本关系和公理为基础的数学体系内，在定义、定理之间进行形式推理，理解构造和发展整个体系的逻辑结构，能理解并分析相互之间的逻辑关系。譬如学生会从不同的定义出发来研究平行四边形的所有性质与特征构成的整个系统，进而揭示各种定义的等价性；学生也能理解哪些事实必须当作公理而接受，再在此基础上导出所有合乎形式逻辑的结论。     4-水平：严谨 其特征是学生领会了现代公理系统的严密性，对于几何对象的具体性质以及几何关系的具体含义都可以不作解释，而是完全抽象地建立一般化的几何理论，这实质上已经将几何提高到一个广泛应用的领域。譬如学生能比较各种公理体系，并能不用具体的几何模型来研究各种几何学。也只有在达到了这一水平的基础上，才能进而将公理化思想渗透进数学的各个不同分支，从而使数学形成一个严谨而完美的形式逻辑演绎体系，暂时离开它所依据的具体现象、客观事实，而从内在的逻辑联系中，进一步探讨数学科学的深奥的本质结构。     根据儿童的思维发展与学习过程提出来的这一思维水平理论，正好相应于数学教学中应该体现的"数学化"思想。一般来说，在某一个水平上进行的组织活动，往往成为下一个水平的研究对象，通过重新组织又提高到一个新的水平。数学教学这一活动过程，就应该是教师根据社会现实的需要与儿童认识过程的发展规律，在不同阶段提出学生应该达到的不同水平，并且引导学生不断地攀登新的水平；就在这不断提高水平的过程中，学生研究着各种不同的数学现实，学会了各种不同层次的数学化，从而也通过这条途径掌握了数学。     在根据思维水平理论以体现"数学化"思想的数学教学过程中，还必须强调以下几点：一是思维的直观性。抽象而复杂的数学知识，总以某些具体对象或内容作为现象背景材料，形形色色的不同层次的数学化，总要以某个相应的数学现实为出发点，因此在数学教学过程中，必须时刻牢记学生所拥有的数学现实，鼓励学生的直觉思维，尽可能阐明问题的来龙去脉，从而在学生头脑中形成一个具体而鲜明的原型，这样才能形成掌握数学化思想的扎实基础。二是思维的阶段性。处于不同思维水平阶段的学生，往往拥有不同层次的数学现实，掌握着不同形式的数学语言，也具有不同程度的数学化水平。一般而言，超越其现有水平而作盲目的跳跃式的提高，往往会适得其反，欲速则不达；或者是仅仅从表面上掌握了某些东西，而对其内在实质却一无所知或是一知半解。只有遵循思维发展和认识过程的规律，在不同的思维水平阶段，提出各种不同的数学化要求，才能真正循序渐进并获得预期的成果。三是促进和加强学生的反思活动。直观的思维会形成很多新的发现，可这些发现要成为真理，就要具有逻辑演绎的严格依据，就必须依赖于对自己的判断、想象进行不断的反思，以直观形象为背景，以演绎推理为工具，反复地思考，反复地推敲。一个人对自身经历的活动的反思是提高认识水平、促使思维发展的核心，对推动人们深入地认识事物的本质，起着非常关键与重要的作用。例如学生也许凭眼睛观察就可以得出平行四边形对角线互相平分这一直觉形象，可是如果促使学生考虑一下为什么，对这个结论有意识地进行反思，可能会得到意想不到的收获；有些学生会从逻辑推理的角度，从平行四边形的性质来推证，因而在建立演绎体系上前进了一步；也有些学生会以图形结构的眼光，将平行四边形绕中心旋转180°与自身重合而得出这一结论，如果继续将反思推进到更高水平上，就会更进一步发现对称、反射以至变换、映射等概念。正是环绕着这一连串的直觉思维、反思、表达、判断，不断地将数学化过程推向前进，而这也正是数学的教与学过程所追求的目标。