美国中学数学改革四十年     近四十年来，美国中学数学经历了一次革新和一次倒退（重回基础）。美国数学教育界内外的最新报告都指出，今天美国又面临，或者说应当进行第二次革新。 现在美国所处的状况很多地方与四十年前一样，对学生的成绩不满；纯数学和应用数学的最新发展在中学数学课程中没有反映；受到足够训练能理解和掌握最新技术的职工太少。而今天在计算机和经济的竞争中美国又受到日本和西欧的挑战。     为了更深刻地认识现在的形势，美国教育家提出，应当接受波利亚的忠告，研究四十年前所遇到的问题，吸取上一次革新和倒退的教训，作出正确的决定。 数学革新     新数运动的口号--发现法，严格推理，数和数字分析，整体结构--都是伊利诺伊大学1951年提出的奋斗目标。据美国中学数学研究会报告，新数运动教学大纲中用得最多的代数课程是从芝加哥大学40年代确定的课程发展而来的；几何课程是从希尔伯特和伯克豪夫的工作发展而来的。     上次革新之前，中学数学的情况很不理想。学生的数学基本功很差（对学生的基本功我们从来就不满意）。今天相信40年代50年代"老数学"很成功的人，忘记了新数运动发展的主要原因就是要提高学生的理解力和数学技能。     美国大学入学数学考试委员会1959年的报告提到，当时的数学课程落后于数学理论及其应用的发展。报告指出，本世纪初数学的发展已经使数学的各个分支成为统一的整体。集合、函数、数系和逻辑起着重要的作用。不等式开始与方程并列，立体几何与平面几何结合在一起，三角不再独立而成为二年级代数的一部分，它不是从几何中推导而是从代数中推导出来。解析几何几乎不再作为一门独立的课程，斜率放到一年级代数中，二次曲线放到二年级代数中了，其它内容，例如心脏线、玫瑰线和其它特殊曲线都被删除了。     今天，发现法没有被广泛采用，数量分析不受重视，除了有一点几何，集合和数系在今天的课程中很难找到。不过课程结构的改变多数被保留下来。很少有学校还把立体几何和解析几何分开来教，斜率还是在高一代数中教，二次曲线留在高二代数，三角与代数还是一起教。因此，现在美国和加拿大绝大多数学校的高中数学课程中都有新数运动的反映。可见课程结构的改变比数学内容和教学方式的改变更容易保留。 成绩下降     新数运动被认为是60年代后期和整个70年代学生成绩下降的原因。从某些测试得知成绩下降是肯定的，但这究竟是为什么却并不清楚，聘请SAT－M作解题测验，请NAEP作个体测试，请ITBS作技巧测验，请NLSMA作比较研究，所有此类研究都证明公众的看法并不正确。     数学素质测试（SAT－M）的设计是评估学生      （1）理解数学的基本概念和较高深的概念的能力；     （2）应用已有知识学习新知识的能力；     （3）用学过的知识观察问题、解决问题的能力。     SAT－M并不强调知识的记忆、数学运算的熟练，而只注意确定要求学生达到的最低限度能力的标准。因此，SAT－M不是计算技能测试，而是解决问题能力的测试。这样，SAT－M不能算作高中数学测试。但是SAT－M仍是反映高中数学课程质量、教学质量和学习质量的气压表。SAT－M平均分最高的年度是1962－1963年度，直到1969－70年度以前，成绩下降不算快，低于1953－54年度那一年的下降。1967－68年度直到1978－79年度成绩持续下降。从那以后，平均分几乎保持不变。     罗得里克（Roderick）对1936年、1951－55年、1973年IOWA大学生参加的测试作了比较。他的报告指出，1963年的学生，无论是6年级还是8年级，各科成绩都比1973年的学生好。他得出这样一个结论：对大多数目标来说，新数运动的数学课程及其教法都是严重不足和无效的。但贝克曼（Beckman）1970年从42所中学的1296个学生测试109个算术题和几何题，结果1951年度平均分是45.7，而1965年是54.9，有明显的进步。1975年USLE作的一个范围更广的研究也得出不同于公众的结论。这一研究指出，1974年度中学生的计算能力与10年前的同龄人一样。第一次NAEP数学测试于1973－74年度对26到35岁的成人（他们学的都是"老数学"）和13到17岁的学生（学的是新数学）进行对比，发现能力差别不大。尽管NAEP考试时间对成人不限，对学生考同样的题并且限时。NAEP的数据说明了什么？如果对新数运动的批评是正确的，那么13到17岁这一组计算技能应当较低。而数据表明13岁的孩子可以完成成年人所做的大多数计算，17岁的还可以做得更好。 1962－66年，SMSG承担NLSMA测试。这一时期内，同时用新老两种模式的教学大纲教学，以便对比。这一测试涉及11万学生，作了充分的分析，得出的报告有33卷，然而它的结果没有引起公众的注意。SMSG的学生，也就是学了新数运动的学生，虽然计算技能稍逊一筹，但理解力、分析问题和解决问题的能力更强，因此，SMSG以牺牲一点算术技能为代价，得到了更多的回报。 倒退     专家对这一革新是相当满意的。然而由于测试结果得不到全面的宣传，公众开始不满意考试成绩的滑坡了，这个滑坡被归咎于新数学大纲。有人打出一张标语："乔妮为什么不会做加法？"于是有人提出了一个诱人的口号"回归基础"。今天在许多地方都有倒退，强调用纸和笔来计算的技能。     与新数运动一样，回归基础也取得一些成效，这个运动建立了升级和毕业必须达到的最低限度能力测试。这种测试常常只考笔算能力。      然而，这些成效付出的代价很大。最好的25%的学生的计算能力下降了。各种技能中应用和解决问题的能力从1972－73年度到1977－78年度就开始下降，直到1981－82年度仍不见改进。NAEP主席指出这种倒退："一个时期以来公众特别强调基础，而评估数据却表明学生的数学能力下降了，解决问题的能力、理解概念的能力尤其下降得多。"     对好学生来说，SAT－M测试数据也指出这一倾向，应用题测试的平均分持续下降，一直到1978－79学年度，后来再没有显著的回升。     以下例子说明计算能力和理解能力不是同一回事。1981－82年，有57%的13岁学生，72%的17岁学生能够正确计算同时给出下面这种乘法问题的精确答案： 估计3.04×5.3的值约为：（a）1.6； （d）1600；（b）16； （e）不知道。（c）160；     然而，不计算只作估计就只有20%的13岁学生和36.6%的17岁学生给出了正确答案。其中还包括随机乱勾搭按在内。     60年代，不少中学的学生，都使用同一种教材，而这种教材更适合尖子生。到70年代，这种情况翻转过来，所有学生也都用同一教材，而这种教材更适合差生。可见，所有的学生学习同一种教材是很不现实的。 如今面临的大问题     无论对新数运动或回归基础怎么看，大家都同意，现在的高中数学存在很大问题。最大的问题就是，大量的甚至是多数高中毕业生缺乏必要的数学知识去面对社会，胜任他们喜欢的工作，胜任必须的岗位培训。      产生象这样被广泛认同的问题一定有许多因素。下面七个方面可以反映这一点。     1.高中数学内容中的一些很简单的问题，不少学生都答不对。例如，报告表明只有53%的高中生学过一年几何，而学过几何的学生中又只有52%能答对这样一个简单的问题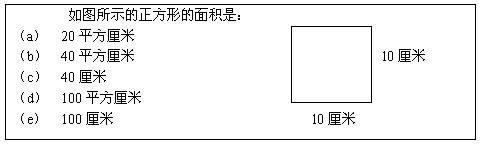：      那么，高中阶段不再学几何的那47%的学生的知识会是什么样呢？     2.有许多高中生好象从来没有上过数学课。答不出上面这样问题的学生几何肯定会遇到麻烦。对要学几何的84个班级的学生考查他们本应具备的几何证明能力，发现有29%的学生连最起码的三角形全等的证明都写不完全。必须指出，证明的能力依赖于其它许多实际的知识。     一年级代数的不及格率可能比几何的还要高。有许多学生看起来很聪明地不上代数和几何课，他们知道自己达不到学及格的水平。这样一来，不改数学课程，不改变入学学生的知识水平只一味提高高中数学课的毕业要求，只会增加不及格率和逃课率。对此必须有一定措施。     3.总的来说，高中生没有上够数学课。     4.即便上过一年代数、一年几何的学生也可能懂得不多。     5.高中和大学生中需要补课的人数之多是个警告。大约40%的高中一年级学生登记读普通数学和代数初步，这表明他们没有学过9年级标准的代数课。1980－1981年度两年制大学报告中有42%的学生登记补习算术，普通数学，初级和中级高中代数，高中几何，初等函数。大学和4年制学院分别有18%和24%的学生也是这种情况。     高中阶段往往对初中所学的数学知识不满。大学阶段又对高中所学的数学知识不满。学生不具备学习社会科学、商业、心理学等课程所需的较复杂的数学知识。     6.即使学过三年数学的学生，很多也没有学会应用自己所学的数学知识。我们用NAEP1977－78年度出的另一道题来看：有人提出用下面这个公式来确定1-7岁男孩的标准体重：W＝17＋5A 其中W是标准体重，A是男孩的年龄，由这个公式，男孩每长一岁增加多少体重？     对这样一个问题，没有学过代数的人中有53%答对，学了一年代数的人中有58%答对，学了两年代数的人答对的有64%。这样看来学了两年代数的学生只有11%学会了线性关系基本性质的简单应用。     对13个中学二年级代数班的调查表明，同意"数学对现实生活很有用"的学生，一年级比二年级要多。这说明，相当多的聪明学生学的只是古希腊时期早已有过的东西。他们把本来在各种领域都有很大用处的一门学科学成死板无用的课程了。     7.除了代数、几何和分析之外，数学中很多重要的分支都被忽略了。1972－73年度NAEP出了两道概率题，其实这两道题只用到一点算术知识：掷三次硬币，有两次正面向上，问第四次掷，正面向上的可能性是多少？正确回答1/2的，13岁学生只有15%，17岁的有17%，成人有46%。     8个红球，6个绿球，2个白球放在一个坛子里，第一次么出白球的可能性是多少？下面那一个公式给出正确答案？（a）1/（8＋6＋4）；（b）1/（8＋6＋4＋1）； （c）1/（8＋6＋4＋2）； （d）2/（8＋6＋4＋2）；（e）不知道。给出正确答案（d）的，17岁的有31%，成人只有28%。     专家们认为：现实生活中经常用到的实例，课堂里不教。当学生遇到这些问题的时候，他们就得再去学.有些学生是会去学，而有些学生则完全放弃应用。 反倒退     1975年，有数学会理事会任命的一个小组，美国国家数学教育启发式委员会（NACOME），号召大家不要用那些只讲计算技术、计算机、统计及其应用的教材。他们推荐的十年制教材的内容求：     a）保持数学主要框架的逻辑结构，     b）保持为完整地理解抽象概念所需的基本概念，     c）为学生提供知识，使他们将来能把数学尽可能地应用到实际生活中去，用到自然科学和社会科学中去，用到专业领域和消费领域中去，也就是用来解决一切可能用到数学的问题。     d）熟悉数学符号、形式化等常用的数学方法，了解它们的用途局限性，     e）最迟不晚于8年级末，就要让所有的学生学会用计算器，允许学生用计算器完成数学作业。     f）所有的学生，而不是有能力的学生，都要学计算机；         ·中学计算机课不限于只学习计算机指令和操作系统；          ·计算机文化课应当包括让学生具备应用计算机的经验。     g）各级各类学校都要十分注意把分数、小数的教学放在优先地位，要组织好对学生的测试和对教学的评估。     h）统计思想的教学要贯穿于初中、高中阶段的各门课程之中.     为了实现这个理想，NACOME号召修订地方教材。几乎同时，美国国家教科所NIE在俄亥俄的欧几里得召集了一次教育工作会议，会上确定数学教育的十大基本目标：     （1）提高计算机操作技能；     （2）会建立数学思想和物理现象的联系；     （3）会进行近似计算；     （4）能建立和解释数据库，学会应用图表；     （5）学会测量，包括选定相关性质，选定精确度，选用适当的仪器，应用仪器进行测量的技术，以及系统内数量单位的转换；     （6）会选择有用的结果；     （7）会定性地分析变化的快慢、产生变化的因素，并从中得通结论；     （8）懂得有关概率的概念；     （9）会运用计算机，由直接经验感知计算机的能力和局限；     （10）有解决问题的能力。     解决问题的能力也被看作是唯一的目标，它可以代替其它所有的9项目标。     欧几里得会议也被称作基本技能会议。一年以后，美国国家数学监理会发表一篇文章，把欧几里得会议所确定的目标就叫做"基本技能"。其实这是一个策略，它把人们所要求的回归基础作了一点文字上的修改，这样一来，解决问题被提到基本技能的首位，当作数学学习的主要目的，其它目标也被重新排列，使用计算机的能力提到第五位，第七个目标被删掉，替代它的是对几何的要求。      不久以后，美国国家教师协会综合了人们的许多建议，发出一份文件称为"80年代行动纲领"。这一行动纲领提出8条建议中有4条与教学大纲有关：     （1）解决问题是80年代美国中学数学的目标；     （2）数学的基本技能要比计算机专业所需的更广泛；     （3）数学课程要使毕业生的计算能力和使用计算机的能力得回到全面提高；     （4）需要进行更多的研究以设计一种更加灵活的、为众多学生的不同需要提供更多选择的课程。      所有这些文件都给出同一个信息，回归基础是一个危险的运动，应该制止。如果这些文件中提出的建议都被采用，结果一定会使中学数学来一次更大的革新。 响应     "80年代行动纲领"一文提出，高中毕业生所学的三年数学应有如下内容：         （1）掌握几何、代数的基本概念。     （2）会用初等概率和统计。     （3）会在日常生活中应用数学知识。     （4）会估计、测量和验证计算结果的误差。     除了为升大学所用的传统内容，数学课还应对那些不打算立大学的学生给予同样重视。对于平衡工程来说，数学是6个基本领域之一，没有数学知识其它所有领域中的基本能力都不可能学会，各大学对数学基础的要求描述如下会应用数学技巧解决日常生活中实际问题，知道什么时候、怎么应用这些技巧；     熟悉数学语言、符号、推理，并能严格定量地绘出表达式；     具有应用计算机、计算器的能力；     熟悉统计、统计原理的基本概念；     掌握一定程度的代数、几何、函数的知识。     除了这些内容之外，还有一些大学入学所指定的内容，学习学、工程、高等数学课程和计算机科学所需要的内容。     数学教育界内外的报告几乎一致同意，高中数学课必须作两点根本的修改。第一，学生的能力必须提高，毕业要求一定要提高，重点要提高解决问题的能力，而不是死记硬背的能力，学生则既要提高基础知识的水平又要增强解决问题的能力。第二，课程必须更新，近似估计、数学应用、计算机和概率在高中数学中应占主要地位。 革新，而不是小的改变     现在的期望是，三个学年--两年代数、一年初等数学分析，包括三角学。能使每个好学生既学到基本概念又学到计算技能，除非按"危险的信号"一文的建议加长中学学制，或减少几何课时，或提前学代数，否则就没有必要的课时按这些报告的要求来提高学生的能力。但是没有报告提议减少几何课，也没有报告提议早一点学代数。就算加长中学学制以增加提高的课程，仍然没有时间添加新的内容而不去掉另外一些重要内容。这样看来，尽管过去十年中有这么多报告提出相同建议，他们的目标仍然只是一个无法实现的梦想。但是有一阵狂热一一一一一计算机执行符号演算的能力实际上可以完成具有算法特征的任何一项工作。现行软件可以具备现在所教的代数和初等分析课的内容，以及几乎所有的演算技巧。     就象多功能计算器使算术课原来必须的笔算教学不再必要一样，计算机软件也使代数学中必须熟悉的笔算技术不再必要。只要删掉几个题材就可减少可观的课时。平均来说，一年级代数课中至少有1/3的课时是有关二次三项式或其它多项式的因式分解，及其对有理式的应用。这个内容对大多数学生来说是毫无用处的。即便在没有计算机以前也没有用处。现在我们有更多理由来删除这一内容。     计算机技术的充分发展迫使教学大纲作更实质性的改动，使微积分失去重要地位。     反对使用计算器和计算机来作计算的争论出现了，有人认为传统的笔算技巧是理解概念所需的。然而技巧和理解是两种不同概念。比如人们不理解机械的重要概念而照样学会修理机器的技术。同样，尽管我们不知道重要的技巧，可照样学会了充满概念的数学。我们学会了三次方根，却并没有人作很多开三次方的笔算，很少有人用无穷序列计算对数或三角函数值精确到小数点后三到四位。我们有一些人根本不知怎样用这种方法去计算，但我们仍然可以利用查表或计算机给出的对数和三角函数值，并觉得很了解这些数值的意义。数学的历史就是解决数学难题的技术日益发展，使它们方便易行的历史。通常这种发展的过程有利于摈弃繁琐的计算，使数学概念变得易于理解。      除了几何之外，教会学生微积分计算技巧仍然在高中数学中占支配地位。但是，1980年，打算学工程自然科学的大学新生中只有则认为微积分起关键作用，而打算学计算机科学、商业、社会科学的新生中的则认为，复杂的数学还是有用的，但微积分并不重要。      事实上，最新技术的充分应用迫使教学大纲作更实质性的变动，使微积分原来的目标和课时安排失去其重要地位。简而言之，数学知识的缺乏是如此严重，数学领导的改变是如此明显，以至于若再不改变高中数学的目标和性质就不能满足现在的学生对数学的需求。最近的报告断定现行的大纲需要作彻底检查而不是作小的改动，需要革新而不是倒退。 [参考文献] *钟善基指导 程艺华编译自"The Secondary School Mathematics Curriculum，1985yearbook"PP1－22.