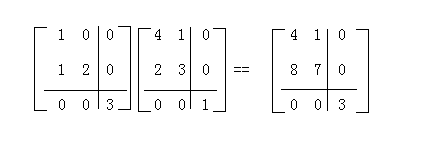
4-4-1-2 接上
2) 逆矩阵(与群中逆元素概念对照)

若AA^-1= A^-1A = E（单位矩阵），则A^-1为A的逆矩阵。

只有方阵才有逆矩阵；

若|A| = 0, 则A为奇异矩阵，其逆矩阵无法确定；

若|A| ≠ 0，则A为非奇异矩阵，具有唯一的逆矩阵。

3）共轭矩阵(与群中共轭元素概念对照)

A、B、X为三个矩阵，若A = X^-1BX，则称A与B为共轭矩阵。

* 共轭矩阵具有相等的迹。

4）矩阵乘法的一种特例

当处理的矩阵，所有非零元素都在沿对角线的方块中，这时矩阵乘法情况特殊，例：

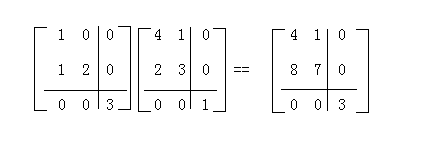
该积矩阵最明显特征是，按照乘因子矩阵完全相同的形式划分为方块。不难看出，这种类型的结果必定是恒成立的。

此外，还可看出积矩阵中给定方块的元素只由乘因子中对应方块的元素所决定。

因此，当两个方块形式相同的矩阵相乘时，每个矩阵中的对应方块可独立于其余方块加以考虑。