6-2-2-2-1
2、σ轨道杂化方案
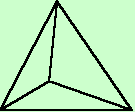
首先以四面体分子为例说明如何确定一组σ杂化轨道由哪些原子轨道组成的。其他分子的σ轨道杂化方案与之类似。
(1)四面体分子AB4(Td群),[CoCl4]2-
第一步,确定原子A的四个杂化轨道,其中每个轨道的瓣指向B原子,并以四个杂化轨道的集合(或四个B原子上指向A原子的σ轨道的集合)作为分子点群(Td)表示的基,确定该表示的特征标。确定特征标的规则为:
①操作不使杂化轨道(波函数)改变,特征标χ=1;
②操作使杂化轨道(波函数)改变符号,特征标χ=-1;
③操作使杂化轨道(波函数)与其他轨道(波函数)变换,特征标χ=0。
简言之,以一组杂化轨道为基的表示的特征标的简化计算规则为:
特征标=不被操作移动的轨道数目。


恒等操作,χ(E)=4, C3操作,χ(C3)=1,
对C2、S4和σd用同样方法处理,得χ(C2)=0,χ(S4)=0,χ(σd)=2.
第二步,根据Td群不可约表示特征标表(表6-2),利用约化公式将可约表示约化:
|
Td |
E |
8C3 |
3C2 |
6S4 |
6σd |
||
|
A1 |
|
1 |
1 |
1 |
1 |
1 |
|
|
A2 |
|
1 |
1 |
1 |
-1 |
-1 |
|
|
E |
|
2 |
-1 |
2 |
0 |
0 |
(z2, x2-y2) |
|
T1 |
|
3 |
0 |
-1 |
1 |
-1 |
|
|
T2 |
|
3 |
0 |
-1 |
-1 |
1 |
(xy,xz,yz) (x,y,z) |
约化:由约化公式
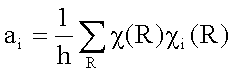
a(A1)=1/24(1×4+8×1×1+3×1×0+6×1×0+6×1×2)=1
a(A2)= 1/24 [1×4+8×1×1+3×1×0+6×(-1)×0+6×(-1)×2]=0
a(E)= 1/24 [2×4+8×(-1)×1+3×2×0+6×0×0+6×0×2]=0
a(T1)= 1/24 [3×4+8×0×1+3×(-1)×0+6×1×0+6×(-1)×2]=0
a(T2)= 1/24 [3×4+8×0×1+3×(-1)×0+6×(-1)×0+6×1×2]=1
约化结果Γ=A1+T2
这说明组成杂化轨道的四个原子轨道中,必有一个是属于A1表示的原子轨道,另三个为属于T2表示的三个原子轨道。
第三步,由特征标表的Ⅲ区中轨道的多项式标记确定轨道的变换性质:
|
A1 |
T2 |
|
s |
(px、py、pz) |
|
|
(dxy、dxz、dyz) |
可有两种组合:
sp3(s、px、py、pz)
sd3(s、dxy、dxz、dyz)