|
当前位置:学习内容 - 第六章 刚体力学 |
|
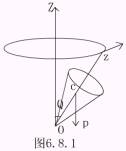
(6.8.8)式也可由下面方法得到。当陀螺的自转角速度 陀螺对定点O的角动量L可写成
这就意味着,在近似理论情况下,可以认为总角速度w、角动量L的方向与对称轴Oz的方向相同。因此,角动量L在空间的变化决定了陀螺对称轴在空间的运动。 这就意味着,在近似理论情况下,可以认为总角速度w、角动量L的方向与对称轴Oz的方向相同。因此,角动量L在空间的变化决定了陀螺对称轴在空间的运动。
由于对称轴与角动量L一起以 与(6.8.11)式比较,知道 由此得到 解得
写成矢量形式,有
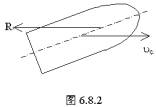
可见(6.8.13)式就是(6.8.1)式。 高速陀螺和一个允许其自转轴任意取向的悬架就构成了回转仪。由(6.8.13)式知,当外力矩不为零时,回转仪将以进动角速度 2.应用举例 (1)利用回转仪的定向性,可保证飞机、导弹、火箭或鱼雷等在预定的航线上飞行。 (2)从枪筒中射出的子弹,在飞行中要受到空气阻力的作用。要使子弹在飞行中不偏航、不翻转,保证能击中目标,且在击中目标时弹尖在先,也要利用高速陀螺的回转效应。 如图6.8.2所示,设空气阻力为R,其方向与子弹质心的速度方向相反,但一般并不作用在子弹的质心上,R对质心C的力矩使子弹绕过质心的水平轴转动,从而使子弹翻转。为了避免子弹翻转,在枪筒内侧有螺旋式的来复线,使子弹离开枪筒后绕对称轴高速旋转。这样,空气阻力的力矩就使子弹轴线沿子弹飞行方向(-R方向)进动,子弹的轴线与前进方向保持不大的偏离,并且击中目标时总是弹尖在先。 |