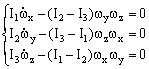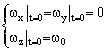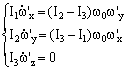当前位置：学习内容 - 第六章 刚体力学

§6.9 刚体转动的稳定性

1．刚体稳定转动的必要条件

刚体转动的稳定性是指刚体在转动过程中它的角速度的大小和方向均不随时间变化。由欧勒动力学方程可知，只有作用在对称刚体上的外力矩为零时，才可能出现刚体的稳定转动。但这还不是刚体稳定转动的完整条件。因此仅有外力矩为零这个条件并不能保证转动是稳定的。可以证明，刚体稳定转动的必要条件有二个：外力矩必须为零；初角速度必须沿惯量主轴方向。

外力矩为零时的欧勒动力学方程为

(6.9.1)

为简单起见，设t=0时刚体仅绕Oz轴转动，即

(6.9.2)

把上式代入(6.9.1)式得

积分上式并利用初始条件(6.9.1)式，可得

即 (6.9.3)

这就是说，刚体在运动的任何时刻，角速度w必须沿着初角速度方向，而这一方向是刚体惯量主轴的方向，因为由初始条件(6.9.1)式知道，刚体开始运动时转动轴线是惯量主轴之一。这就证明了刚体稳定转动的二个必要条件。

2．刚体转动的稳定性

下面要讨论的问题是，在满足上述稳定转动的条件下，如果刚体受到微扰使转动轴稍微偏离原来的方向(惯量主轴方向)，这种偏离能否不越来越大。如果能保证偏离不越来越大，则称这种转动是稳定的，否则就是不稳定的。即讨论刚体受微扰后的角速度

(6.9.4)

中的能否在任何时刻都比小得多。

假设在任何时刻都比小得多，那么，与比较，、和均为一阶小量，它们的乘积是可以忽略的二阶小量。在此条件下，将(6.9.4)式代入(6.9.1)式得

(6.9.5)

由上式第三个方程立即得到

=常数

将式(6.9.5)的第一方程对t微商，再将第二个方程代入，便得

或写成 (6.9.6)

其中常数k为 (6.9.7)

若k>0，则(6.9.6)式的解为

这个式子说明，只要微扰终止时比小得多，则在以后的任一时刻均保持很小。

方程(6.9.6)是谐振方程。这就是说是以小振辐(由初始条件决定)作角频率的谐振动。

若k≤0，由式(6.9.6)的解可知，将随时间按指数规律增加或线性规律增加，转动的稳定性被破坏。

同样讨论，可得其满足的方程为

式中的k与(6.9.6)式相同。显然也是以小振辐作谐振动，因此和稳定性条件相同。

由以上分析可知，如果微扰终止时、和均比小得多，则当k>0时，即

I₃>I₁ I₃>I₂

或

I₃<I₁ I₃<I₂

时，转动是稳定的，否则就不是稳定的。第一种情况对应于转动轴是最大惯量主轴，第二种情况对应于转动轴是最小惯量主轴。可见，在三条惯量主轴不相等的情况下，刚体绕最大或最小惯量主轴的转动都是稳定的，而绕转动惯量是中间值的惯量主轴的转动是不稳定的。当I₁=I₂¹I₃时，绕x和y轴的转动都是不稳定的，只有绕z轴的转动是稳定的。

上一页 下一页