理论力学网络课程

当前位置：学习内容 - 第六章刚体力学

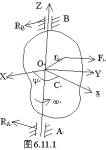
§6.10 刚体定轴转动时支点上的动反作用力

刚体定轴转动是最常见的一种运动，定轴转动的刚体可以看作是其上有两个点(A、

B)静止不动的刚体。AB就是转轴。轴在这两点处受到轴承的限制，轴承对刚体的作用可以用轴承对轴的约束反力代替。刚体在A点处所受约束反力为N_A，分量表示为N_Ax、N_Ay和N_Az；在B点处所受约束力为N_B，分量表示为N_Bx、N_By和N_Bz。设有n个主动力F_i(i=1,2…n，)作用在刚体上，作用点位矢为r_i，再设刚体的质心C到转轴的距离OC=l，且OA=a，OB=b，取O为坐标原点，用x轴和y轴的夹角表示刚体绕z轴转动的角位移。如图6.10.1所示。

虽然刚体定轴转动只有一个自由度，用一个转动方程就可求出刚体的运动，但该方程中不包括约束反力，约束反力要用质心运动定理和对O点的角动量定理来求。

角动量定理来求。这两个定理共有六个标量方程，其中只有一个(即角动量定理的z分量方程)不包含约束反力，是定轴转动方程，而从其它五个方程中可求出约束反力。刚体的质心运动定理和对O点的角动量定理为

(6.10.1)

(6.10.2)

刚体定轴转动时的角动量L的一般表示应为

(6.10.3)

应该说明的是，刚体定轴转动时角动量L和角速度w的方向不一定一致。只有当转动轴是惯量主轴，从而I₁₃=I₂₃=0时，角动量和角速度方向才一致，这时。

将(6.10.3) 式代入(6.10.2)式，再把(6.10.1)式和(6.10.2)式写成分量形式便得到刚体定轴转动的动力学方程：

(6.10.4)

(6.10.5)

(6.10.6)

(6.10.7)

(6.10.8)

(6.10.9)

(6.10.9)式不含有约束反力，不必和其他方程联立即可独立求解。在解出刚体运动之后，可用它们求约束力，但约束力共有六个分量，所以不能完全求解。在轴方向的约束力只能由(6.10.6)式求出其合力N_z=N_Az+N_Bz，而不能分别确定N_Az和N_Bz的大小。从物理上看，这是由刚体的性质决定的，因为如在A、B点沿方向分别加上任意一对大小相等、方向相反的力并不影响刚体运动。若在转轴方向除重力外没有其他主动力，当转轴水平时，有N_Az=N_Bz=0，而当转轴为铅直方向时，有N_Az=Mg，N_Bz=0。

当，时所算出来的N_A和N_B与时算出的结果相差很多。称前种情况的约束反力为动反力。后种情况的约束反力为静反力。由方程(6.10.1)、(6.10.2)与(6.10.4)、(6.10.5)可以看出，刚体转动时所受的约束反力与约束力矩不仅与刚体转动角速度有关，而且与刚体质心偏离z轴的位置x_c、y_z及刚体的惯量积I_yz、I_zx有关。只有当

x_c = 0， y_c = 0 及 I_yz = 0， I_zx = 0

时，动约束反力及力矩才等于静约束反力及力矩。X_c=0，y_c=0说明转轴必须通过质心，而I_yz=I_zx=0说明转轴必须是惯量主轴。两个因素结合起来，即当刚体定轴转动时，刚体所受的约束反力及反力矩与静止时相等的条件是：转轴必须是中心惯量主轴。