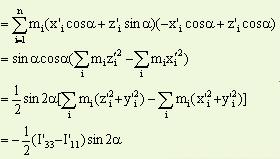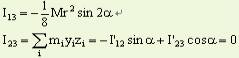当前位置：学习内容 - 第六章 刚体力学

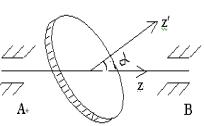
刚体绕中心惯量主轴转动时，轴承上不出现附加轴压力。所以刚体绕这种轴转动时，即使没有轴承约束，也能继续绕轴转动。我们称刚体不需要外力矩维持绕一固定轴作匀角速转动的运动状态为转动平衡状态，并称这种转轴为自由转动轴。显然，对非自由转轴，如果没有轴承的约束，刚体就要改绕其它轴转动。

对于高速运转的机件的制造与安装，要特别注意动平衡问题。为了达到动平衡，常常需要在转动部分的适当位置增加或减少(如钻孔等)一些质量。

例 涡轮可以看作是一个均质圆盘。由于安装不善，涡轮转动轴与盘面法线成交角a=1°，已知涡轮质量为20千克，半径r=0.2米，重心在转轴上，O距离轴承A与B的距离各为
a=b=0.5米。设轴以12000转/分的角速度匀速转动，试求轴承上的压力。

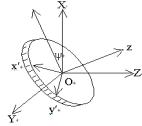
[解] 如图6.10.2所示，由于圆盘中心O的法线O¢z和转动轴OZ不重合，因此转动轴不是惯量主轴。由于质心在转轴上，故有l=0。

为了便于计算，我们取如图6.10.3所示的坐标系，其中OXYZ为固定坐标系，OZ为转动轴，沿水平方向。Oxyz坐标系固结在圆盘上，且Oz和OZ重合。为Ox和OX两轴的夹角，即为圆盘角速度w。Ox¢y¢z¢是由圆盘的三个对称轴组成的坐标系，Oz¢与OZ轴的夹角为a，这样由方程(6.10.4)、(6.10.5)、(6.10.7)和(6.10.8)可得

(1)

(2)

(3)

(4)

显然，我们求出I₁₃和I₂₃后，就可从上四式中求出约束反力N_Ax、N_Ay、N_Bx、N_By。下面我们来求Oxyz坐标系中的I₁₃和I₂₃。

图6.10.2	图6.10.3	图6.10.4

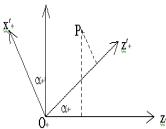
在图(6.10.4)中，Oy和Oy¢轴是重合的，两个坐标系都固结在刚体上，因此它们之间的关系与圆盘运动无关。Oxyz和Ox¢y¢z¢的变换关系为

匀质圆盘有

所以把它们代入(3)和(4)式，最后由方程(1)、(2)、(3)、(4)求得

将所给数据代入，得每轴承上的动反力为

而每个轴承上的静反力只有10千克，动反力要比静反力约大54倍，可见动反作用力对轴承的危害是很大的。

上一页 下一页