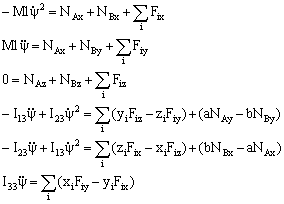当前位置：学习内容 -小 结

小 结

I．刚体运动的微分方程

1．刚体运动的广义坐标

2．刚体一般运动的微分方程

(质心运动定理)

(对定点或对质心的角动量定理)

(动能定理)

动能定理可以作为辅助方程。

II．力系的简化与刚体平衡

1．力系的简化 空间任意一力系总可以简化为通过某点(简化中心)的一个主矢F及主矩M。主矢与简化中心选取无关。主矩与简化中心选取有关。

2．刚体的平衡方程 F=0， M=0

III．欧勒运动学方程

1．欧勒角、、是描述刚体作定点转动时的三个独立变量。

2．欧勒运动学方程

IV．惯量张量与惯量椭球

1．刚体绕一直线的转动惯量

式中

，，

叫作刚体对x轴、y轴及z轴的转动惯量，而

，，，

叫做惯量积。a、b、g则为转动轴线的方向余弦。

2．张量与并矢

(1)惯量张量l是个二阶张量，有九个分量，其惯量矩阵有九个元素，对角元素为转动惯量，非对角元素为惯量积。

(2)并矢——按一定顺序排列的两个矢量，如AB，一般情况下，AB≠BA。

AB=A_xB_xii+ A_xB_yij+ A_xB_zik+ A_yB_xji+ A_yB_yjj+ A_yB_zjk+ A_zB_xki+ A_zB_ykj+ A_zB_zkk

惯量张量l可写成

式中E为单位并矢

刚体定点转动的动能可以写成

n为w方向的单位矢量。因此，转动惯量I又可写成。

3．惯量椭球与惯量主轴

(1)惯量椭球方程

(2)选取惯量椭球主轴为坐标轴，惯量积全部为零，这些轴叫做惯量主轴。或说，使惯量张量对角化的轴叫做惯量主轴，而相应的对角元素I_xx、I_yy、I_zz叫做主转动惯量。

(3)均匀刚体的对称轴就是惯量主轴。

(4)惯量主轴和主转动惯量可通过求解本征方程的方法得到，所得的本征值就是主转动惯量，而本征矢量的方向就是惯量主轴的方向。

4．刚体的角动量及转动动能——以定点O或质心C上的惯量主轴为坐标轴时

V．刚体平面运动动力学

1．动力学方程 ， ，

2．滚动摩擦

VI．刚体定点运动力学(欧勒动力学方程)

欧勒动力学方程

VII．拉格朗日陀螺

1．I₁=I₂¹I₃，重心在动力对称轴上。

2．运动一般由自转、进动及章动合成。如无章动，则叫规则进动。

IX．高速陀螺近似理论

当陀螺的自转角速度比进动角速度大得多时，进动角速度的大小为

利用高速陀螺的定向性，可进行导航等。

X．刚体转动的稳定性

1．刚体稳定转动的必要条件

刚体稳定转动的必要条件有二个：外力矩必须为零；初角速度必须沿惯量主轴方向。

2．刚体转动的稳定性

当刚体绕Oz轴(转动惯量为I₃)转动时，如果

I₃>I₁，I₃>I₂，

或 I₃<I₁，I₃<I₂，

则转动是稳定的。也就是说，刚体绕最大惯量主轴或最小主轴的转动是稳定的。绕转动惯量是中间值的惯量主轴的转动是不稳定的。

XI．刚体定轴转动时支点上的动反作用力

1．刚体定轴转动的动力学方程

2．由于转动，在轴上产生了附加压力，即使是主动力全部为零时，它也不等于零。通常称为动压力。只有当转动轴通过刚体的重心并且是惯量主轴时，附加压力才等于零。

上一页 下一页