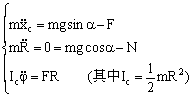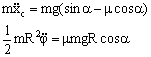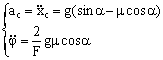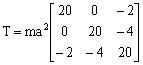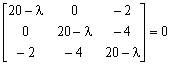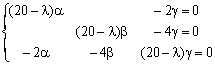|
当前位置:学习内容 -综 合 例 题 |
|
综 合 例 题 例6.1 轴为水平的均匀圆柱体沿着倾角为a的粗糙斜面下滚(见例题6.1图)。已知圆 柱体的质量为m,半径为R,并略去滚动摩擦。试求出圆柱体的运动情形。(1)假设没有滑动。(2)假定有滑动发生,而滑动摩擦系数为m。 [解] 取坐标系如图,假定在t时刻,质心坐标为(xc,R),柱体的转角∠ACC0=j(当质心位于oy轴上的C0点时,半径CA与x轴平行)。N与F分别为约束反力与摩擦力。 (1)滚而不滑的情形。此时,应满足约束条
按方程(6.5.1),得圆柱的运动方程为 例6.1图
由(1)式得
及
由(4)式中的第二式看出:圆柱沿斜面下滚时,质心加速度 由于无滑动时摩擦力F<mN,故由(5)和(3)式求得实现纯滚动所必须满足的条件为
或
(2) 且滚且滑的情形。如果条件(6)不满足,则产生滑动,因而(1)式不成立。但是此时的摩擦力应为极大值,即
因而
这就是说,在目前情况下,质心以加速度ac运动,同时柱体本身以角加速度 积分(7)式,求出
则uc即为柱体与斜面接触点P的滑动速度,可称为圆柱体的滑动速度,利用(7)式看出
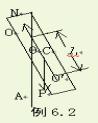
因此,此时条件(6)必不满足,可见,按触点的滑动速度将随柱体沿斜面下滚而不断增大。 例6.2 设质量为m的复摆绕通过某点O的水平轴作微小振动,试求其运动方程及振动周期。 [解]
复摆又叫物理摆,日常中看到的钟摆就是复摆。在右图中,O是悬点,OC=l为悬点到质心C的距离。设此复摆绕通过O点的水平轴线转动,OA为竖直线,OC与OA的夹角q就是复摆绕此定轴转动的角坐标。在复摆上作用着重力P=mg和轴承对它的约束反作用力N。复摆绕OZ轴转动的微分方程为
由于振动是微小的,故有, 式变为
这是标准的谐振动方程,其通解为
两个积分常数A和 振动周期为
这个式子说明,在小摆角范围内,复摆的周期与摆角无关。 例6.3 质量为m、2m、3m和4m的四个质点分别位于坐标系oxyz的(a,a,a)、 [解] 几何中心就是坐标系原点,根据式(6.4.3)和(6.4.4)计算刚架对Oxyz坐标系的张量组元分别为 T11=T22=T33=20ma2, T12=T21=0,
T13=T31=-2ma2, T23=T32=-4ma2。 即惯量张量
在点O的本征值应满足久期方程
或
(20- 由此解出
在点O的惯量主轴方向就是对应于以上各本征值的本征矢量方向,根据式(6.4.2)有
对应于主惯量
本征矢量
对应于主惯量
本征矢量
对应于主惯量
本征矢量
容易判断,三个本征矢量e1、e2、e3即三个惯量主轴是相互垂直的。 |