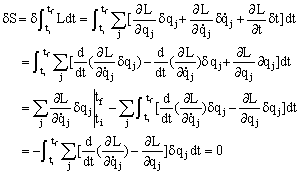当前位置：学习内容 -第七章 正则方程

Y

力学体系中的真实运动是由动力学方程决定的。哈密顿原理可以从各种运动学所允许的可能运动中把真实运动选出来。哈密顿原理可视为力学中的第一原理，以前所得出的各种动力学方程都可由它推导出来。

图7.1.3

O

X

B

A

D

C

为了说明和理解哈密顿原理的应用，现在我们进一步讨论微分符号d与变分符号d是可以对易的。考察在xy平面内的抛射体运动，令AB为真实路径的一部分，而CD为邻近路径的一部分，见图7.1.3。A和C是同一时刻两路径上对应的两点，B和D是另一时刻对应的两点。若A点的坐标为(x,y)，那么C点的坐标为(x+dx，y+dy)而B点则为(x+dx，y+dy)，以A，B两点的坐标表示D的坐标，有

[x+dx+d(x+dx)，y+dy+d(y+dy)]

再以A、C坐标表示D的坐标，则有

[x+dx+d(x+dx)，y+dy+d(y+dy)]

对同一点D，两种表示应相等，因而有

d(dx)=d(dx)，d(dy)=d(dy)

所以说变分算符和微分算符是可以对易的。同样道理，在等时变分dt=0的情况下，d和算符也是可以对易的。这是因为

例1 用哈密顿原理证明重力场中自由落体的真实运动规律是。

[解] 设物体的质量为m，速度为u，则物体的动能和势能分别为和V=-mgz。因此

代入哈密顿原理dS=0，得

变分后得 (1)

括号中的第一项可以写成

故(1)式成为

积分得 (2)

由于对两端固定的等时变分有，因此(2)式中的第一项等于零。又因为对任意dz，式(2)都成立，所以有

积分两次得

例2 用哈密顿原理推导拉格朗日方程。

[解] 因为L=L(q_j，，t)，所以有

由于积分号下的dq_i的任意性，故得

(j=1，2，3…，s)

上一页下一页