当前位置：学习内容 -第七章  正则方程

§7.1  哈密顿原理

1．位形空间、相空间

我们知道，三维空间中一个点的位置可以由三个直角坐标x、y、z确定，这个点的运动方程为

x=x(t)，y=y(t)，z=z(t)

这就是说，此点沿着上述三个方程所限定的三维空间中的一条曲线运动。同样地，由s个广义坐标q₁、q₂……q_s所确定的体系可以看成是s维空间中的一个“点”，即这个点的s个坐标就是q₁、q₂……q_s。这s个q值，就完全规定了该系统的位形，若体系的运动微分程的解是q₁₌q₁(t)，q₂=q₂(t)，…，q_s=q_s(t)，则体系的运动相当于一个“点”沿着上述s个方程所确定的s维空间中的“曲线”运动。总之，任何具有有限自由度的力学系统总可由s维空间的一个特定的“位形点”来表示。而“位形点”的运动就表征着整个体系的运动。因此我们把以s个广义坐标q_j所确定的s维空间叫作位形空间。当给定的力学系统的位形随时间变化时，位形点在位形空间中划出一条曲线轨迹，在这些q彼此独立的一般情况下，该曲线是连续的。

另外，下一节我们会看到，正则方程是2s个一阶方程组，由于方程的对称性，我们取s个广义坐标q_j和对应的广义动量p_j为独立变量，把这些q和p看作是一个矢量的诸分量。因此我们把s个广义坐标q_j和广义动量p_j所确定的2s维空间叫作相空间或相宇。相就是运动状态的意思。力学体系在时刻t的运动状态可用相空间中的一个“点”来代表。相空间中的一个点不仅规定了系统的位形，也规定了由这些p表示的系统的运动状态。当时间改变时，力学体系的运动状态也随之改变，代表点将在相空间中运动。由于力学系统的哈密顿函数H及其微商都必须是单值函数，故相空间中经过任一点的相轨迹只能有一个。当然这里说的是H函数不显含时间的情况。如H函数显含时间，则经过相空间某一点的相轨迹在不同时刻的方向可以不同，所以相轨迹有可能相交。

2．变分原理

现在简要介绍一下计算变分的基本思想。首先考察一个例子，如图7.1.1所示，悬挂在(a，b)和(-a，b)两点之间的一根长度为L的柔软绳索在竖直的xy平面内会形成一

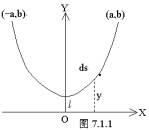
条什么样的曲线呢？它应该是一悬链线(二端固定的均匀重链在重力场中处于平衡状态时链的形状称为悬链线)。下面我们就来求出它的方程。

由于绳索处于稳定平衡，其势能为极小值。若r为单位长度上的质量，并假定为恒量，则一段圆弧的势能将rgyds，在平衡时，积分

          (7.1.1)

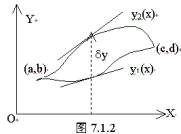
为最小值，这一积分沿曲线从(-a，b)到(a，b)，由于ds为，所以上式可写成

                     (7.1.2)

式中y¢代表y对x的导数。于是，该问题就归结为求得什么样的函数y(x)，才使得V取得最小值。这是一个变分法问题。下面扼要说明解决这一问题所必需的基本思想。

考虑积分

                       (7.1.3)

欲求极大值或极小值，就必须在所有连接(a，b)和(c，b)的曲线中选取一条特殊的曲线。如图7.1.2所示，我们定义变分为y₂(x)-y₁(x)，并记为，即在x相同时y从曲线到曲线之间的变化。对于相同的x，各曲线的斜率一般也是不同的，这种斜率的变化记为。

从图中明显看出，在x从a变到c时，发生了变化，因而是x函数，我们假定这种函数在x=c之间各点上都是连续的。对x求导数，则得

                   (7.1.4)

由(7.1.4)式可知，微分与变分算符是可以对易的，以后我们将经常使用这个微分与变分互换的基本关系。同样可以证明，变分与积分运算也可以互换，即

     (7.1.5)

一般地说，如果改变了函数I中的y因而也就也就改变了y¢，就产生了一个变分。若使I取得极大值或极小值，变分法指出，对于每一个y能够做的任意改变，都有=0。应当清楚和一般微分dy之间的区别：是指当x取某一给定值时，y从曲线到曲线的变化，dy是沿某一给定曲线

由于x的变化而产生的一种微分变化。由变分法知，如果f(x)满足欧勒一拉格朗日方程

                       (7.1.6)

则I将取稳定值，一般是极大值或极小值。

上一页下一页