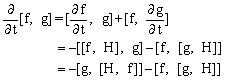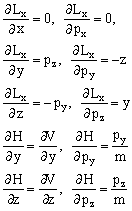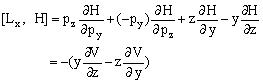理论力学网络课程

当前位置：学习内容 -第七章正则方程

3．泊松定理

如果已知正则方程的两个运动积分

f(q_j，p_j，t)=c₁

g(q_j，p_j，t)=c₂

那么，由它们组成的泊松括号也是运动积分。这就是泊松定理。

泊松定理可分两种情况证明，如果力学量f和g不显含时间t，证明比较简单。

在泊松恒等式

[f，[g， h]]+[g，[h， f]]+[h，[f， g]] = 0

中，令h=H(哈密顿函数)，则有

[H，[f， g]]+[f，[g， H]]+[g，[H， f]] = 0 (7.3.18)

由于f=c₁，g=c₂，按(7.3.5)式有

[f， H]=0， [g， H] = 0

因此(7.3.18)式中的后两项等于零，(7.3.18)式成为

[H，[f， g]] = 0

再按(7.3.5)式，则有 [f， g] = c₃

如果力学量f和g显含时间t，则由

f = c₁，g = c₂

得 (7.3.19)

(7.3.20)

再由泊松括号的性质(5)有

(7.3.21)

式中第三步应用了泊松恒等式。

把(7.3.21)改写为

根据(7.3.5)式条件，有 [f，g] = c₃

因此[f，g]也是体系的运动积分。

利用泊松定理也可以得到运动积分，但不一定得到新的运动积分。例如，若广义动量p₁和p₂是两个运动积分，根据泊松定理，[p₁，p₂]也是运动积分。但根据基本泊松括号可知[p₁，p₂] = 0是一恒等式。以零作运动积分没有什么用途，所以在求正则方程的积分时，并不能完全依赖泊松定理。

例1 试用泊松括号证明有心力场中质点的角动量L是运动积分。

[证明] 若角动量是正则方程的运动积分，则有

如L不显时间则有，因此只要证明[L， H] = 0就可以了。

设系统是一个在有势场V=V(x，y，z)运动的质量为m的质点，则哈密顿函数为

角动量的泊松括号为

(1)

由于 L_x = yp_z-zp_y

所以有

把这些关系式入(1)式，可得

根据有心力的性质有

故有 [L_x， H] = -(r×ÑV)_x = (r×F)_x = M_x

同理可得 [L_y， H] = M_y，[L_z， H] = M_z

写成矢量形式，便是 [L， H] = -[r×ÑV] = M

因为有心力对力心的力矩为零，即 M = 0

所以 [L，H] = 0

这就证明了角动量是运动积分，即角动量是常矢量。