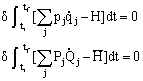当前位置：学习内容 -第七章 正则方程

§7.4 正 则 变 换

1．正则变换

变换理论是研究和求解力学问题的有效工具，每当真接积分运动方程有困难时，我们便试图引入一组新变数，以使问题得到解决。

在§7.2中已经指出，哈密顿函数H是q_j、p_j和t的函数，而哈密顿正则方程是2s个一阶微分方程。如果H中不出现某个q_j或p_j，则这个q_j或p_j就是循环坐标；再根据正则方程，立刻得出相应的q_j或p_j为常数。显然，H中的循坐标越多，得到的积分就越多，这正是人们所希望的。而H中有无循环坐标和广义坐标的选取有关。因此，我们总可以通过变换理论使得在原来没有循环坐标的哈密顿函数H中出现新的循环坐标。比如，由于拉格朗日方程和正则方程的形式与q的选择无关，这些方程对任意的坐标变换( 有时称为点变换)

Q_j = Q_j (q₁，q₂，…q_s，t) (j = 1，2…，s) (7.4.1)

保持形式不变(Q_j为新坐标)，因此，只要适当选择Q_j，使其具有较多的循环坐标，就能使问题易于解决。但是对正则方程来说，正则变量P和q是具有同等地位的独立变量，所以坐标变换应扩大到包括把独立的坐标和动量q_j，p_j同时变换到新的Q_j、P_j的变换，它们的变换方程为

(7.4.2)

一般说来，由方程(7.4.2)所规定的任意变换(时间t作为参数)不一定是正则变换。当正则变量q、p变换为Q、P时，如果正则方程保持形式不变，那么这种变换称为正则变换，即 (j = 1，2，…，s) (7.4.3)

其中表示新的哈密顿函数。

2．母函数

如前所述，正则变换并非是随意的，而必须具有一定条件。下面从哈密顿原理求出正则变换的条件。由(7.2.1)式有

再根据(7.1.10)式写出旧、新坐标表示的哈密顿原理，即

要使以上两式同时成立，必须两式的被积函数相差一个特定函数F的全微分，例如，我们可设F=F(q_j，Q_j，t)，则有

(7.4.4)

或 (7.4.5)

式(7.4.5)就是正则变换的必要和充分条件，函数F在积分上、下限的变分为零，它是联系新、旧正则变量的函数。当F为已知时，可由式(7.4.5)求出未知变量p_j、P_j和H，或者说，正则变换关系可由函数F来确定。因此F被称为正由变换的母函数。

3．四种形式的正则变换

从表面上看，F是(4s+1)个变量q_j、p_j、Q_j、P_j、t的函数。但是由于变换关系(7.4.2)式的限制，F实际上只是(2s+1)个独立变量的函数。除t之外，其余2s个变量可组成下面四种母函数： F₁(q_j，Q_j，t)， F₂(q_j，P_j，t)

F₃(p_j，Q_j，t)， F₄(p_j，P_j，t)

(1) F₁(q_j，Q_j，t)，这是通过q_j和Q_j进行的正则变换。由于

将该式与(7.4.5)式比较，立即得到

(7.4.6)

(2) F₂(q_j，P_j，t)，这是通过q_j和P_j进行的正则变换。显然，在式(7.4.5)两端加添一项之后，便得

(7.4.7)

选取q、P、t为独立变量。并令

将(7.4.7)式与

相比较，便得到由母函数F₂所表示的正则变换：

(7.4.8)

用类似方法，不难得到如下另外两种形式的正则变换。

上一页下一页