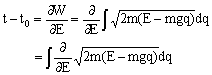理论力学网络课程

当前位置：学习内容 -第七章正则方程

保守场情况下的H-J方程解题步骤如下：

(1) 写出体系的哈密顿函数H(q_j，p_j，t)；

(2) 将H中的p_j改为，写出H-J方程

(3) 解出哈密顿特性函数W(q₁，…，q_s，E，a₂，…，a_s)，它含有s个非相加的积分常数。

(4) 用W作正则变换的母函数F₂，其中积分常数E，a₂…，a_s，作为变换后的“动量”，变换后的哈密顿函数H=E=常数，这样，所有的“坐标”都是循环坐标。

(5) 按第二种母函数F₂的变换公式求出此时的变换公式

(j = 1,2,…,s)

(j = 2,3,…,s)

即用新坐标b_j代换Q_j，用新动量E，a₂，…，a_s代换p_j。到这里变换后新的正则变量已经解出(全是常数)，并且按变换公式回到原来旧的正则变量的求解也全部完成。

例自由落体在t₀时从q₀高度下落，t时刻到达q高度，试由哈密顿—雅可比方程求证

[解] 这是最简单的一维问题，没有约束，且H中不显含t。先求运动积分q=q(t)。

第一步：写出H=H(q，p)

(1)

第二步：将H(q_j，p_j)中的p_j代以，写出H-J方程

(2)

由于这里只有一个广义坐标，W=W(q)不必分离变量就可直接解出W。

第三步：解出W

故得 (3)

此处不必求出积分。

第四步：写出所需的运动积分。由(7.6.16)式得

(4)

因为E是总能量，当q = q₀时，p = 0，故由(1)式可知。

E = mgq₀ (5)

代入(4)式得 (6)

在(7.5.16)式的运动积分中，t₀本为待定积分常数，故(6)式积分时的积分常数可并入t₀中。设t₀即为本题的初始时刻，则(6)式正好满足初始条件t = t₀，q = q₀。由(6)式可得

若把q改为习惯符号z，则上式成为

或

由于本题只有一个自由度，故积分常数只有E及t₀两个。