位置:第五章第三节
|
第三节 适应数学新课程理念的中学数学教学模式 |
事实上,数学教育中对直观能力的培养,开始总是从对实物的直观,或对图形的直观,这是毫无疑问的。但是随着学习内容的不断深入,对图形性质的直观,对命题的直观就越来越重要了。仍以几何学习为例,随着几何学习的水平的提高,对直观的要求也越来越高。如图5—2所示,对实体的直观可以得到图形,对图形的直观可以得到图形的有关性质,对图形性质的关系的直观可以得到命题。
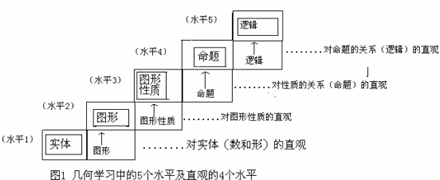
从以上的启示中不难发现,《教学论稿》中提出的直观性原则“是为处理好教学中词概念和事物及其形象之间的矛盾而提出的”观点,忽视了“直观是全部认识的基础”,“知识是主体自发活动的产物”这些直观主义的基本理念。当然更没有意识到人的直观能力是随着学习水平的提高而不断提高的。
2、数学教学中的活动主义
由于受历史的局限性,裴斯塔洛奇提倡的直观主义教育思想也有许多不完善之处。例如“知识是主体自发活动的产物?”,还是“主体有目的活动的产物?”就是一个重要的分歧。
杜威(Dewey)所提倡的活动主义(activism),从教育哲学的角度发展了裴斯塔洛奇的直观主义教育思想 。
杜威在1895年发表的“数的心理学”(psychology of Number)中对数的产生,有如下的论述:“数不只是通过感觉就可以理解事物的性质,不是客观事物外在显现的属性在头脑中的反映。客观事物在数观念的建立中起到的是辅助作用,事物并非数。”他认为“数是主体为了达到自己的目的,通过(认识)活动,在思想中建立起来的”,“数是儿童有目的的活动的产物”,“数是在思想上对客观事物的处理方法中产生的”,杜威以上对数是怎样产生的论述,可以看作是具有划时代的重要意义,是对裴斯塔洛奇直观主义的发展。
把杜威提倡的“在做中学”(learning by doing)简单的看成“儿童中心论”是“实用主义的代表”,并没有从认识论作分析,特别是缺少从学习心理学的角度进行深入的研究,致使没有真正理解杜威活动主义教育思想的实质。诚然,什么叫“活动”?活动怎样和知识的获得相联系?时至今日,仍然是应当研究的问题。但是,皮亚杰(Piaget)对活动的解释,应当是指导当今数学教学的一个重要理论基础。
3、数学教学中的建构主义
皮亚杰(Piaget)认为:“认识起因于主客体之间的相互作用,这种作用发生在主体与客体之间的中途”即主客体之间密切的相互影响。“首先是存在着主体到客体,客体到主体之间起着中介作用的中介物”,他认为“一开始起中介作用的并不是直觉而是可塑性要大得多的活动本身”。
皮亚杰在1941年发表了“关于儿童数概念的发生”(lagenese du nombre chez l` enfant ,Delachaux et Niestle,1953 )是关于认识论方面的基础性研究。皮亚杰的最大贡献,用他的学生C.Kamii女士的话说 “他把知识化分为物理的、社会的和逻辑数学的三大类。数学知识和物理知识,社会知识形成的过程是不同的。他认为数学知识必须根据儿童的自身活动,在思想上形成的。这种活动不能被他人所代替。只能让儿童自己主动去建构。这是皮亚杰对数学教育的最大贡献,也是培养实践能力、创新精神教学模式的理论基础。
皮亚杰在数概念的形成活动方面,提出了两种感觉运动的活动 ,其一是“Classification”,其二是“Seriation”。前者是指把对象视为“同一”的分类,集中的活动,后者是找出对象之间的“差异”按照某种顺序的排列活动。皮亚杰还提出了操作(operation)的术语。这种操作并非指实际的(actual)活动,它已转化为指头脑中思考的(vitual)活动。
这两种活动具有不同的性质,皮亚杰又提出了“可逆性”,“结合性”的术语。例如,实际活动的行为像“覆水难收”一样不可逆转,但是头脑中思想上的操作(operation)可以像电影胶片一样可以逆转,他把这种可逆性作为头脑中思想上的操作行为的特性。
结合性方面,比如前面提到的称为“同一”的分类,集中的活动和找出对象之间的“差异”,按顺序排列的活动就是有结合性。这种结合性表现在视为“同一”的同时,又要看到“差异”,这样多次的操作在相互结合的过程中,从整体上,形成一种知识的体系。这是皮亚杰的认识论的一个显著特征。
皮亚杰不仅对数的概念,对空间、图形的有关概念,对概率统计中的有关概念的发生、发展都有论述,其基本观点和数的概念的形成发展一样,都是由“儿童的亲身活动建构起来的”。
从上面可以看出,皮亚杰的“活动主义”又把杜威的“活动主义”推向了一个新的阶段——建构主义。
建构主义的理论基础是皮亚杰的发生认识论。“活动”是皮亚杰发生认识论中的一个基本概念。“活动”是知识的源泉,又是思维发展的基础。因此,在数学教学中必须突出学生的数学学习活动。
皮亚杰对诸多数学概念的发生、起源的研究,对数学教育的贡献,目前是无人企及的。但是,皮亚杰的研究所遗留的问题,应当成为我们今后极其重要的研究课题。
1、皮亚杰的研究(理论),对指导儿童的数学学习是有效的,但对指导高年级学生的数学学习中,存在诸多问题。 这有可能是因为对从具体操作活动阶段向形式操作活动阶段转移的过程,研究尚不深入所至。
2、一旦形成概念以后,通过思想上的操作活动向更高级的概念的形成过程,也就是说高级数学思维活动和皮亚杰提出的操作活动之间相同之处都应当是“主体的自主活动”,但两种活动的区别,尚无实证的研究。尽管目前对反省思考(reflective thinking)给予了极大的关注。
以上两个方面大概应当是数学教育领域对建构主义理论研究中亟待解决的课题。
直观主义、活动主义、建构主义对数学教学影响很大,可以看作是三个不同时期的里程碑。要想真正的把握建构主义的实质,把直观主义、活动主义和建构主义联系起来,在直观主义的基础上,逐渐发展成为活动主义,进而在活动主义的基础上又发展为当今的建构主义,从这个意义上去理解建构主义将会更有利于指导数学教学的实践活动。
三、建构主义理论下的数学教学过程的一般模式
根据直观主义、活动主义、建构主义的基本观点,构建数学教学过程的一般模式,从认识论和方法论的角度,可以提出如下基本原理:
原理1(建构原理):数学知识是由认知主体的主动建构活动获得的。
原理2(互动原理):数学知识的建构过程是学习环境中交流、互动的过程。
原理3(协定原理):数学知识的建构是学习共同体之间达成的“协定(agreement)”。
原理4(反省原理):数学的建构活动以操作的反省思考(reflective thinking)为中心。
原理5(相互作用原理):数学的建构活动,是通过“学习共同体”之间的相互作用实现互动,从而使数学认知结构不断调整完善。
原理6(转换原理):数学的建构活动通过不同的表现形式的转换来实现协定。
这种不同的表现形式相互转换如下图所示:
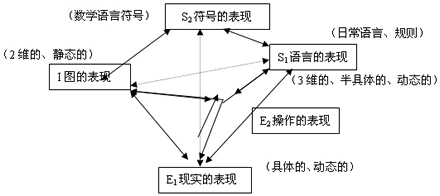
图5—3数学建构过程中的“E→I→S”表现形式及关系
在国内许多数学教育学著作的有关数学学习理论中,虽然也运用了“认知”、“建构”的观点,提出了数学学习过程的三个阶段,即所谓输入阶段、新旧知识相互作用阶段、操作阶段。如图5—4所示。