下载

位置：第六章第三节  

例7  说出你能想到的关于如下两个图形之间相同和不同的地方。

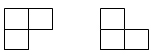
这个题目的设计在于考查学生是否抓住了图形的关键特征。一个补充的问题还可以是要求学生回答什么差异是这两个图形之间最重要的差异。

3、重视对学生发现问题和解决问题能力的评价

《标准》的总体目标强调结合有关的知识技能培养学生解决简单问题的能力，重视培养学生的“数学思考”和“解决问题”的能力。使学生在学习数、图形和统计等的过程中，发展数感、空间观念和统计观念，初步学会多角度提出问题、理解问题，并能综合运用所学的知识和技能解决问题。体验解决问题策略的多样性。在学习数学过程中，建立和提高发现问题和解决问题能力是数学素养的重要标志。通过考查学生发现问题和解决问题的能力，了解学生数学学习的过程和方法。学生的数学学习必须建立在对数学认识的基础上，而不仅仅是掌握一些概念和技能，它包括调查和推理的方法，交流的手段以及对数学知识来龙去脉的理解。也就是说，学生在数学学习过程中需要经历探索、推测或猜想、以及有效的推理去解决有关数学的问题。在传统的教学和评价中，学生解决问题的策略是与例子结合在一起的，对于具体的策略是如何帮助我们思考问题的却很少接触。《标准》中明确地把“形成解决问题的一些基本策略”作为一个重要的课程目标，强调数学教学中必须通过讲解、示范和实践等方式帮助学生获得有关解决问题的策略，而且，这些策略性知识还应该被评价，如同概念和技能一样。

对解决问题能力的评价，一个方法是使用如同波利亚那样的框架作为指导。了解学生是如何理解这个问题的？是否有一个明确的解题计划？解题步骤是否正确或合理？每一步是否正确？他们是否对解法进行了检查或概括？或者确认它是否符合问题的条件？在评价的过程中对每一个指标赋予一定的分值，比如理解3分，计划3分，步骤2分，答案2分等等。

评价的另一个方法是基于一般的对问题解决性质的理解，比如期望学生能够使用解决问题的方法调查和理解学习的内容，即在解决问题的过程中学习数学；从数学内部或外部的情境中发现并提出数学问题；尝试从不同角度分析问题，发展和应用各种策略解决问题；体会到与他人合作解决问题的重要性；用数学语言清楚地表达解决问题的过程，并尝试用不同的方式(文字、字母、图表等)进行表达；根据最初的问题情境证实和解释结果的合理性；对解决问题的过程进行反思，获得解决问题的经验或将解法或策略概括到一个新的问题情境中去；从有意义地使用数学中获得信心等。

教师可以根据学生在这些问题上的表现，给予定性评价。

除了对发现问题和解决问题过程加以评价外，也可以通过纸笔测验对学生分析和解决问题的能力加以考查。纸笔测验的内容和形式，也应依据《标准》确定的目标和内容，以及提倡的评价理念进行改革。改变以往题目单一、机械模仿、形式单调等弊端，尝试运用灵活多样，富于思考，条件灵活和答案多样的题目。在编制试题时，应与现实生活密切联系，问题具有思考性和一定的开放性。下面这样的问题是应当提倡的。

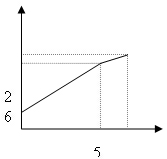
例8 一个农民带若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，售出土豆千克数与他手中持有的钱数（含备用零钱）的关系如图所示，结合图像回答下列问题：

（1）农民自带的零钱是多少？

（2）降价前他出售每千克土豆的价格是多少？

（3）降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱（含备用零钱）是26元，问他一共带了多少千克土豆？(摘自吉林省2002年中考试卷)

这样的问题用到的数学知识和技能并不难，但需要学生理解实际问题，需要学生具备一定的解决问题的意识。同时在解决问题的过程中，学生能够体会数学在现实生活中的应用。