分形无处不在,山川、河流、云朵、曲折的海岸线、美丽的雪花、大脑皮层皱褶、血液微循环管道……均
是分形,同样,彭罗斯拼砌、各种多孔材料、金属裂纹、聚合物、渗流集团……也是分形。自然界或实验室中
许多体系都涉及到分形结构,分形理论为研究这些复杂对象的基本特性及内在规律提供了简明的方法,所取得
的成果令人瞩目。分形理论架起了沟通结晶材料与无序系统之间关系的桥梁。
2、豪斯道夫的维数定义
所谓“维数”是抽述一个对象的几何特征的无量纲量,它反映几何对象占有空间的程度。通常所说的“维
数”指欧几里得维数,它表示描述—个几何体所需要的独立变量数,例如零维、一维、二维、三维分别表示点
、线、面、体。但是这种简单直观的维数定义对于一些复杂的几何体系难以应用,需要有更普遍更适用的定义
。1919年豪斯道夫(Hausdorff)提出了一种对维数下定义的方法:
我们知道,要测量一个几何体的长度(或面积和体积),必须用“尺子”,所得到的数值与测量时所用“尺
子”的长度单位有关。例如,对于—维的线,当用ε作单位长度来度量时,读数将与ε成反比,得
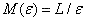
而对于二维的面,则可以用 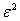 的方块来覆盖它,因此 的方块来覆盖它,因此
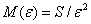
显然,对于三维的体,则有
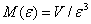
推广到一般形式,对于 d维的几何体,有
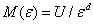
式中 U是ε=1时测量所得到的数值。如果将测量所用的“尺子”的单位长度缩小k倍(即ε变成为ε/ k ),则
该测量所得到的数值放大N倍,变成 NM (ε),有
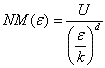
结合 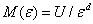 ,可得 ,可得 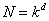
于是 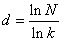 。 。
这样的维数定义具有更深刻的含义,允许的维数可以是分数。常驻用来计算各种分形的维数。
3.分维
分形的维数称为分维,一股不是整数。请看图2给出的典型分形图形。其中(a)为康托(George Cantor)集
合,其形成方法为:取一单位长度直线把它分为三等分,然后去掉中间一段,留下左右两个短线;对每一个短
线重复同样的做法,如此继续下去直至无穷.显然,在每一次分割中所得到的短线都是前一次的1/3。在第n步
后,线段的个数为 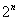 ,每个短线段的长度仅为原来长度的 ,每个短线段的长度仅为原来长度的 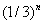 ,即 ,即  ,因此康托线段 ,因此康托线段
的维数为
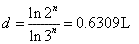
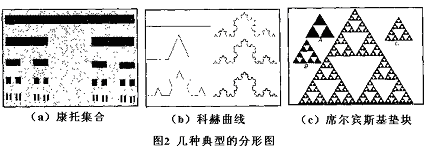
图 (b)称为科赫(Koch)曲线。它是这样构成的:将一长度为 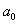 的直线分成三个相等长度的基本线段,用等长 的直线分成三个相等长度的基本线段,用等长
的两个线段代替中间的一段,如此重复下去,始终对新生的曲线的每一线段重复上述步骤。这样就得到越来越
长,且看起来越来越粗的自相似曲线,它好像要覆盖—定的面积。对于第n次迭代的图形,共有 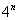 个线段, 个线段,
每个线段的长度为 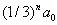 ,所以科赫曲线的豪斯多夫维数为 ,所以科赫曲线的豪斯多夫维数为
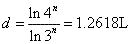
图(c)所示为席尔宾斯基垫块,其构成方法在图中很清楚地显示了出来,它的维数为
<<返回页首>> |

