|
( 1 )声学波和光学波。以一维晶格为例说明晶格振动产生格波。一维单原子链中只有声学波,其色散关系为:
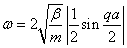
一维双原子链中既有声学波,又有光学波。其色散关系是:
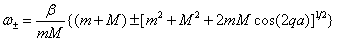
在长波极限(即 q → 0 )情况下,声学波描写原胞质心的运动,光学波描写原胞内不同原子间的相对运动。长波极限下声学波等同于连续介质弹性波。对于长波极限下的光学波,也可在宏观理论的基础上加以讨论,使问题
简化。
( 2 )周期性边界条件。由于晶体结构的周期性,在求解格波的过程中常常使用的一种边界条件是周期性边界条件(又称玻恩——卡门条件),在此条件下,格波波矢 q 不能取连续值,而只能取一系列分立值:
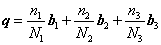
由于色散关系
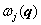 在 q
空间是周期性的,周期为一个倒格矢,即: 在 q
空间是周期性的,周期为一个倒格矢,即:

故只考虑第一布里渊区就可以了。把波矢的取值范围限制在第一布里渊区,则有
晶格振动的波矢数 = 晶体的原胞数
晶格振动的频率数(晶格振动模式数或不同格波数目) = 晶体的自由度数
若设晶格维数是 d (—维、二维或三维)维,则格波可分为 dn 支( n 为原胞内原子数、 dn 为原胞内自由度数),其中 d 支为声学波(特征: 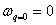 ), d ( n 一1)支为光学波。一般而言,不同支格波的色散关系是不同的.简单晶格只有声学波,而复式晶格必有光学波。 ), d ( n 一1)支为光学波。一般而言,不同支格波的色散关系是不同的.简单晶格只有声学波,而复式晶格必有光学波。
( 3)声子。声子是晶格振动的能量量子,是一个准粒子,其能量为
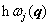 ,准动量为 ,准动量为  。这个准粒子是玻色子,满足玻色统计,其平均声子数为: 。这个准粒子是玻色子,满足玻色统计,其平均声子数为:
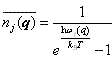
引入声子的概念后,晶体可视为声子气系统。在简谐近似下,声子间无相互作用,可视为理想气体,考虑非简谐效应后,声子间存在相互作用。
( 4 )爱因斯坦模型和德拜模型。利用晶格振动的量子理论,可以很好地解释低温时的固体比热容问题。其简化模型有爱因斯坦模型和德拜模型。爱因斯坦模型假定所有振动模频率相等,可定性解释低温比热趋近于零的问题,但定量上不正确;德拜模型以连续介质中的弹性波代替晶体中的格波,在低温下很好地解释实验给出的 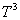 规律。 规律。
( 5 )非简谐效应。固体的许多性质是由非简谐效应引起的,如热膨胀和热传导,因而要考虑势能的非简谐项。非简谐效应导致格波间互不独立,表现为声子间的相互散射或产生或湮灭。声子碰撞时满足能量守恒和准动量守恒:
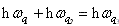
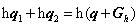
这里,
 时为 N 过程, 时为 N 过程,
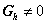 时为 U
过程。 U 过程在涉及声子散射的物理过程中起关键作用。 时为 U
过程。 U 过程在涉及声子散射的物理过程中起关键作用。
( 6 )光子(或中子)与声子的相互作用。用声子的概念不仅可以解释晶体的热学性质,而且可以研究光子、中子等与晶体的相互作用。其相互作用过程可以理解为光子(或中子)与晶体中声子之间的碰撞过程。在碰撞过程中,同样遵守能量守恒和准动量守恒。利用这一性质,可以从实验上测定晶格振动谱。 |

