|
若一维原子链是由质量不等的原子相间排列而成,则原子的振动又会出现新情况。为简便,这里考虑由两种不同原子构成的一维复式格子,相邻同种原子的距离为 2 a
( 2 a 为复式格子的晶格常数),如图 3-2-1 所示。 质量为m的原子位置序号为…,2n-1,2n+1,2n+3 …,质量为 M
的原子位置序号是:…, 2n-2,2n,2n+2…;这里我们假设M>m,类似于方程(3-2-1),得到
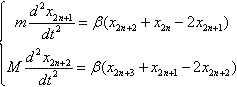 ( 3-2-1 ) ( 3-2-1 )
若晶体有N个原胞,则有2N个方程,方程数等于晶体的自由度数。对于这组方程,仍然采用类似于式(3-1-12)的试探解,则有
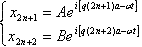 ( 3-2-2 ) ( 3-2-2 )
即认为同种原子的振动相同,只有位相上存在差别,不同原子的振幅可以不同。把式(3-2-2)代入(3-2-1)式
中,可得
 ( 3-2-3 ) ( 3-2-3 )
这是一组齐次方程。若 A
, B 有非零解,则其系数行列式一定为零,即
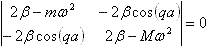 ( 3-2-4 ) ( 3-2-4 )
由此可得出:
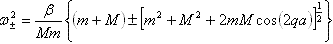 ( 3-2-5 ) ( 3-2-5 )
上式即为一维双原子晶格中格波的色散关系。 |

