|
了解晶格振动模密度的意义不仅局限于晶格热容的量子理论。实际上,计算所有热力学函数时都要涉及到对各个晶格振动模的求和,这就需要知道模式密度函数。以后还会看到,在讨论晶体的某些电学性质、光学性质时,也要用到晶格振动模式密度函数。根据式( 3-5-12 ),我们可以定义:
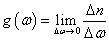 …………………………………………………………( 3-6-1 ) …………………………………………………………( 3-6-1 )
Δn 表示在 ω — ω+Δω 间隔内晶格振动模式的数目,如果在
q 空间中,根据 ω ( q )= 常数作出等频面,那么在等频面
ω 和 ω+Δω
之间的振动模式的数目就是 Δn 。由于晶格振动模(格波)在 q
空间分布是均匀的,密度为 V/2π3(V为晶体体积
),因此有:
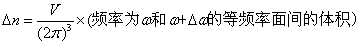 …………( 3-6-2 ) …………( 3-6-2 )
如图 3-6-2 所示,等频面间的体积可表示成对体积元 dsdq
在面上的积分:
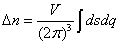 ………………………………………………………………( 3-6-3 ) ………………………………………………………………( 3-6-3 )
|

|
其中 dq 表示两等频率面间的垂直距离, ds
为面积元,显然
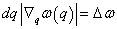
因为
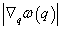 表示沿法线方向频率的改变率。因此 表示沿法线方向频率的改变率。因此
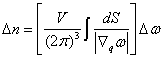 ………(
3-6-4 ) ………(
3-6-4 )
从而得到模式密度的一般表达式
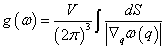 …………(
3-6-5 ) …………(
3-6-5 )
|
|
|
图3-6-1
钾的模式密度与德拜近似模式密度的比较 |
|
|
|

