设函数在区间[a,b] 上有n+1个互异点的函数值为

。

则

称为关于点的一阶差商.又将

称为关于点的二阶差商.

一般地，将

                  (2.6)

称为关于点的K阶差商.

在实际中常采用差商表计算各阶差商，其形式如下：

表2-3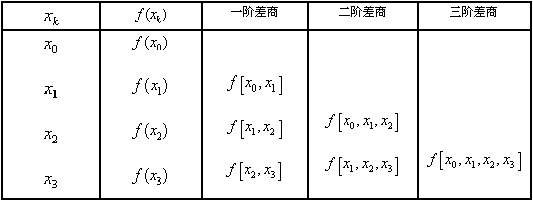

差商具有下列性质：

性质1.n 阶差商可表示为函数值的线性组合，即

此性质可以用归纳法证明.

由性质1.可知，在改变节点顺序时，只是改变右端作和顺序，差商不变，所以有

性质2. 各阶差商都具有对称性，即

性质3.n次多项式的一阶差商为n-1次多项式.

证明设为n次多项式，，将在x点展成泰勒级数，则得

显然，上式右端为n-1次多项式.

性质4. 若在[a,b] 上存在n阶导数，则至少存在一点ξ∈（a,b），使得

证明由至少有n+1个零点，且存在n阶导数。反复应用罗尔定理知至少有一个零点ξ，所以有