设在区间 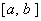 上给定 上给定 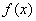 函数表 函数表
求插值函数 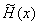 ,使它具有下列性质 ,使它具有下列性质
( 1 ) 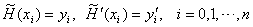 。 。
( 2 ) 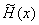 在每个小区间 在每个小区间 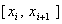 上为不超过三次多项式。 ( 2.23 ) 上为不超过三次多项式。 ( 2.23 )
由两点三次埃尔米特插值多项式得
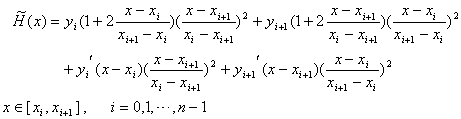 (2.24) (2.24)
将满足条件( 2.23 )的函数( 2.24 )称为 分段三次埃尔米特插值函数 。
分段三次埃尔米特插值函数具有以下的误差估计。
定理 2.4 设 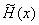 为满足条件 (2.23) 的分段三次埃尔米特插值多项式。若 为满足条件 (2.23) 的分段三次埃尔米特插值多项式。若 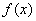 在区间 在区间 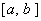 上存在四阶导数, 则对任意 上存在四阶导数, 则对任意 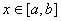 ,总有 ,总有
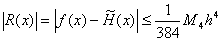 ( 2.25 ) ( 2.25 )
其中 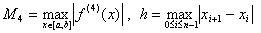 。 。
证明 对任意 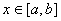 ,必有 ,必有 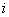 ,使得 ,使得 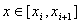 ,由埃尔米特插值余项公式得 ,由埃尔米特插值余项公式得
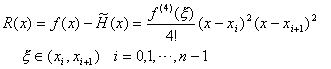
又因为 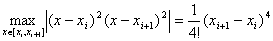
所以 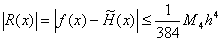
例10 已知函数
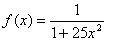
的函数表
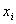
|
-1.00 |
-0.80 |
-0.60 |
-0.40 |
-0.20 |
0.00 |
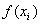
|
0.03846 |
0.05882 |
0.10000 |
0.20000 |
0.50000 |
1.0000 |
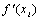
|
0.07396 |
0.13841 |
0.30000 |
0.80000 |
2.50000 |
0.00000 |
试用分段三次埃尔米特插值求 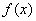 在每个小区间中点的近似值。 在每个小区间中点的近似值。
解 将由分段三次埃尔米特插值公式( 2.21 )得
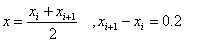
代入分段三次埃尔米特插值公式( 2.21 )得
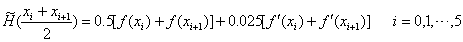 具体计算结果如表 2-8 所示 具体计算结果如表 2-8 所示
表 2-8
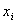
|
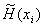
|
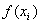
|
- 0.9
- 0.7
- 0.50
- 0.30
- 0.10 |
0.04703
0.7537
0.13750
0.30750
0.81250 |
0.04706
0.07547
0.13797
0.030769
0.80000 |
看出用分段三次埃尔米特插值比用分段线性插值,逼近精度有较明显的改进。
练习 2.4
1. 已知函数表
求分段线性插值函数 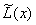 。 。
2. 怎样选择步长 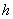 ,才能使分段三次埃尔米特插值函数 ,才能使分段三次埃尔米特插值函数 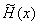 与 与 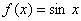 误差小于 误差小于
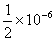
练习题答案
1 . 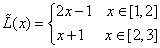
2 .由 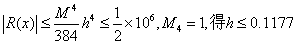
|
|