在高等数学中学习傅立叶级数时,曾提到函数系
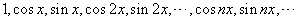 中,由于其中任意两个不同函数的乘积在区间 中,由于其中任意两个不同函数的乘积在区间 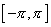 上的积分等于零,则称这个函数系在 上的积分等于零,则称这个函数系在 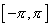 上是正交的,或称这个函数系为 上是正交的,或称这个函数系为 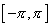 上正交函数系,对于多项式也有类似的定义. 上正交函数系,对于多项式也有类似的定义.
若多项式序列: 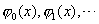 满足条件 满足条件
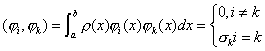
其中 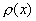 为不恒为零的非负连续函数,则称 为不恒为零的非负连续函数,则称 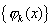 为 为 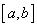 上带权 上带权 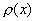 的正交多项式系. 的正交多项式系.
若 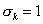 则称 则称 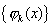 为标准正交系. 为标准正交系.
如果讨论正交时没有说明权函数是什么,就意味着所指的权函数为 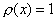 。 。
下面给出正交多项式系几个重要性质:
①任意 n次多项式 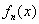 可用正交多项式 可用正交多项式 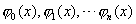 线性表示,即 线性表示,即
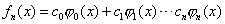 (3.5) (3.5)
其中 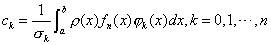
② 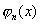 与任意低于n次的多项式 与任意低于n次的多项式 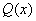 在 在 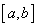 上带权 上带权 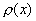 正交,即 正交,即
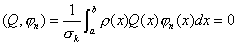
③正交多项式 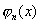 在 在 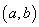 ,内有n个互异实根。 ,内有n个互异实根。
证明 由于 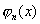 是n次多项式,所以它至多有n个实根.下面来证明它在 是n次多项式,所以它至多有n个实根.下面来证明它在 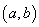 内部的相异实根个数不能小于n,用反证法.假设 内部的相异实根个数不能小于n,用反证法.假设 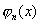 在 在 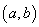 内部的相异实根小于n,那么取出其中的所有奇次重根 内部的相异实根小于n,那么取出其中的所有奇次重根 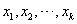 ,其个数一定小于n,因此, ,其个数一定小于n,因此,
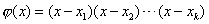 为次数低于n的多项式,而 为次数低于n的多项式,而 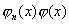 在 在 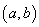 内部不变号,只在有限个点处取零值.所以 内部不变号,只在有限个点处取零值.所以
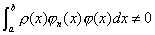
这与性质 2矛盾.故 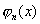 在 在 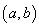 内部恰有n个相异实根. 内部恰有n个相异实根.
④若 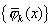 是首系数为1的在 是首系数为1的在 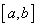 上带权正交多项式系,则 上带权正交多项式系,则
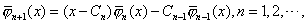 (3.6) (3.6)
其中
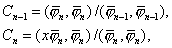
证明 由 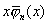 为首项系数为l的n+1次多项式,可表为 为首项系数为l的n+1次多项式,可表为
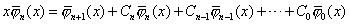
用 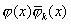 乘两边,积分得 乘两边,积分得
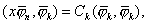
当 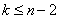 ,时,则有 ,时,则有
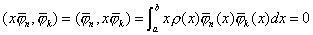
所以 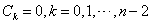
当 k=n-1时,则有
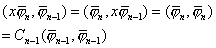
所以
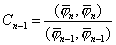
当 k=n时,则有
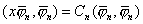
所以 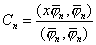
递推公式 (2)对于计算和研究正交多项式是很有用的·
|