设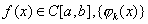 是区间[a,b]上带权 是区间[a,b]上带权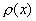 正交多项式,在 正交多项式,在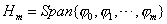
中求最佳平方逼近多项式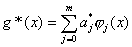 ,根据(3.20)式有 ,根据(3.20)式有
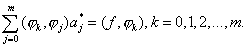
因为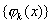 是正交多项武,所以有 是正交多项武,所以有
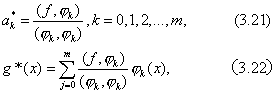
例5 求函数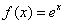 在[-1,1]上的二次最佳平方逼近多项式. 在[-1,1]上的二次最佳平方逼近多项式.
解 因要求在[-1,1]上权为1的最佳平方逼近多项式,故选取勒让德多项式作基底.
设所求多项式为
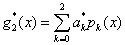
其中
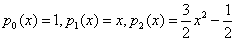
利用(3.21)计算:
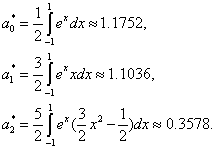
所求二次最佳平方逼近多项式
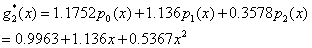
对于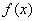 在任意有限区间[a,b]上的最佳平方逼近问题,可应用变换 在任意有限区间[a,b]上的最佳平方逼近问题,可应用变换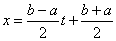 ,将 ,将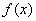 化为[-1,1]上的函数 化为[-1,1]上的函数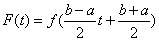 ,然后求出F(t)在[-1,1]上的正交多项式 ,然后求出F(t)在[-1,1]上的正交多项式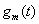 ,于是得到 ,于是得到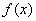 在[a,b]上的最佳平方逼近多项式: 在[a,b]上的最佳平方逼近多项式: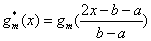
例6 求函数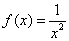 在[0,2]上的一次最佳平方逼近多项式. 在[0,2]上的一次最佳平方逼近多项式.
解 通过变换x=t+2, 将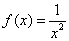 化为[-1,1]上函数 化为[-1,1]上函数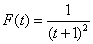 ,设 ,设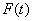 在[-1,1]上最佳平方逼近一次式 在[-1,1]上最佳平方逼近一次式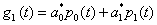 , ,
则有:
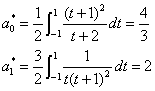
于是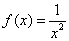 在[0,2]上最佳平方逼近一次式为 在[0,2]上最佳平方逼近一次式为
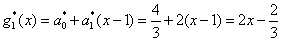
练习3.3
1.求函数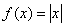 在[-1,1]上的二次最佳平方逼近多项式. 在[-1,1]上的二次最佳平方逼近多项式.
2.求函数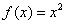 在[0,1]上的一次最佳平方逼近多项式. 在[0,1]上的一次最佳平方逼近多项式.
练习题答案
1. 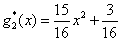
2. 利用变换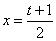 ,将 ,将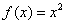 化为[-1,1]上函数 化为[-1,1]上函数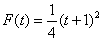 ,计算 ,计算
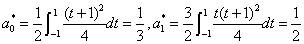
所以
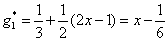
|
|