1.知观测数据:
X |
1 |
2 |
3 |
4 |
Y |
0.8 |
1.5 |
1.8 |
2.0 |
求最小二乘二次多项式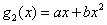
2.解矛盾方程组
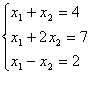
3.求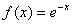 在[-1,1]上二次最佳平方逼近多项式 在[-1,1]上二次最佳平方逼近多项式
4.求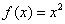 在[1,2]上一次最佳平方逼近多项式 在[1,2]上一次最佳平方逼近多项式
5.试用勒让德多项式表示函数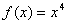
6.测得X的n个值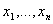 ,通常取平均值 ,通常取平均值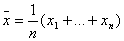 作为X的近似值,其理由是什么? 作为X的近似值,其理由是什么?
7.设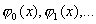 为[a,b]上正交多项式,证明 为[a,b]上正交多项式,证明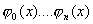 线性无关 。 线性无关 。
习题答案
1.提示: 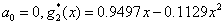
2.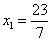 , , 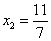
3.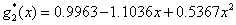
4.利用变换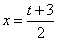 ,将 ,将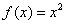 化为[-1,1]上函数 化为[-1,1]上函数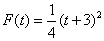 ,计算 ,计算
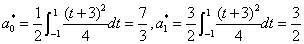
所以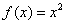 在[1,2]上一次最佳平方逼近多项式为: 在[1,2]上一次最佳平方逼近多项式为:
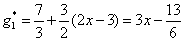
5.设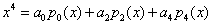
则
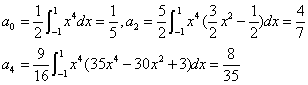
所以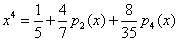
6.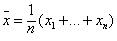 使得 使得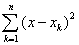 取最小值。 取最小值。
7.提示:设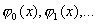 线性相关,则存在一组不全为0的系数使得 线性相关,则存在一组不全为0的系数使得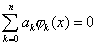
则由正交性得:
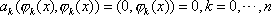
|
|