1.单点弦法的迭代公式
设实函数 在区间[a,b]上单调连续,,且满足 在区间[a,b]上单调连续,,且满足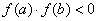 ,则方程 ,则方程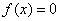 在区间[a,b]内存在惟一实根 在区间[a,b]内存在惟一实根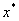 。 。
单点弦法的基本做法是,在区间[a,b]上任意选取互异两点c 和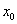 ,过曲线上点 ,过曲线上点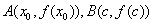 作弦,其方程为 作弦,其方程为
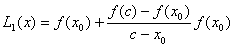
此弦与x轴交点的横坐标为
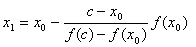
将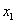 作为方程的根 作为方程的根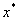 的第一近似值。 的第一近似值。
若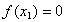 ,则 ,则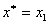 ;否则再过点( ;否则再过点(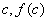 ), ( ), (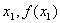 )作弦,此弦与x轴交点的横坐标为 )作弦,此弦与x轴交点的横坐标为
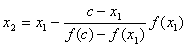
将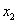 作为方程的根 作为方程的根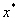 的第二近似值。 的第二近似值。
一般地,如果已求得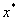 的第n个近似值 的第n个近似值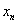 ,则过点( ,则过点(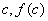 ), ( ), (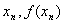 )作弦,此弦与x轴交点的横坐标为 )作弦,此弦与x轴交点的横坐标为
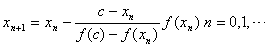 (8.7) (8.7)
将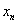 作为方程的根 作为方程的根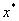 的第n+1个近似值。式(8.7)为单点弦法的迭代公式。 的第n+1个近似值。式(8.7)为单点弦法的迭代公式。
2.单点弦法的收敛性
定理8.2. 设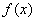 在区间[a,b]上存在二阶连续导数,且满足条件 在区间[a,b]上存在二阶连续导数,且满足条件
⑴ 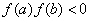 ; ;
⑵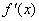 在[a,b]上不等于零 在[a,b]上不等于零
(3)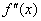 在[a,b]上不变号 在[a,b]上不变号
则选取c是a, b中满足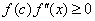 .的一个, .的一个,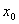 为另一个 则由单点弦法迭代公式(8.7) 为另一个 则由单点弦法迭代公式(8.7)
得到的近似根序列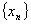 单调线性收敛于方程 单调线性收敛于方程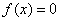 在区间[a,b]内的唯一根 在区间[a,b]内的唯一根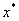 。 。
证明 由条件(1)(2)知方程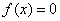 在区间[a,b]内有唯一根 在区间[a,b]内有唯一根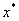 。 。
为了证明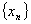 收敛于 收敛于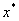 ,先证明 ,先证明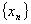 为单调有界序列。 为单调有界序列。
不失一般性,不妨设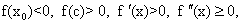 由 由 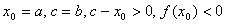 ,可得 ,可得
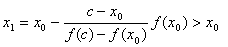
再证明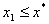 。因 。因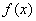 单调上升,所以只需证明 单调上升,所以只需证明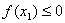 即可。为此构造函数 即可。为此构造函数
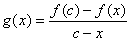
则有 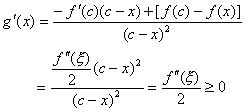
其中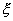 位于 位于 之间。 之间。 为单调上升函数, 为单调上升函数,
由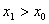 知 知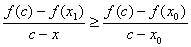
即
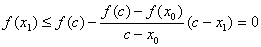
由此证明了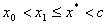
一般地,由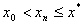 可同样证明 可同样证明
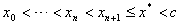
由此得(8.7)产生的近似根序列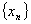 单调上升,且有上界 单调上升,且有上界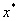 , ,
所以必有极限,设为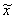 。 。
对式(8.7)两边取极限得
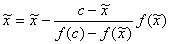
由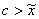 得 得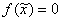
再由方程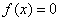 在区间[a,b]内有唯一根 在区间[a,b]内有唯一根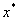 ,得 ,得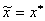
即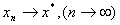
下面证明单点弦法具有线性敛速,为此令
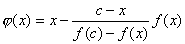
则由式(8.7)得
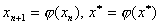
应用微分中值定理得
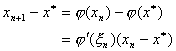
其中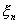 位于 位于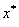 与之间。 与之间。
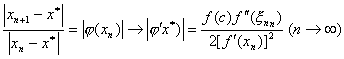
其中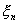 位于 位于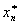 与 与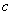 之间。 之间。
当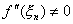 时,单点弦法线性收敛。 时,单点弦法线性收敛。
例4 计算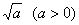 的单点弦法迭代公式,并用它计算 的单点弦法迭代公式,并用它计算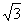 ,准确到 ,准确到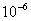 。 。
解 计算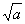 等同于求方程 等同于求方程
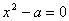
的正根,由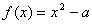 ,代入单点弦法迭代公式(8.7)得 ,代入单点弦法迭代公式(8.7)得
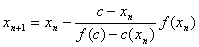
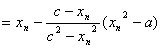
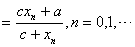
下面用它计算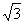 . .
因为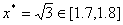 ,在区间 ,在区间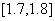 上 上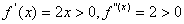 ,选取 ,选取
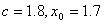
用上面导出的单点弦法公式
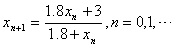
具体计算如表8-4所示:
表8-4
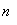
|
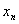
|
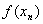
|
0
1
2
3 |
1.7
1.731 428 5
1.732 038 8
1.732 050 5 |
-0.11
-0.002 154 4
-4.16×10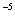
-1.1× 10 10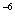 |
因为
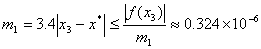
所以
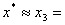 1.732 050 5 1.732 050 5
|