单点弦法在计算过程中只有一个点变动,而另一个点不动,双点弦则是在计算过程中,两个点都变动的更一般情形,见图8-3

图8-3
1.双点弦法的迭代公式
设函数 在区间[a,b]上单调连续,,且满足 在区间[a,b]上单调连续,,且满足 ,则方程 ,则方程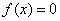 在区间[a,b]内存在惟一实根 在区间[a,b]内存在惟一实根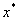 。 。
双点弦法的具体做法是,在区间[a,b]上任意选取互异两点 ,过曲线上点( ,过曲线上点( ), ),
(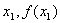 )作弦,其方程为 )作弦,其方程为

此弦与x轴交点的横坐标为

将 作为方程的根 作为方程的根 的第二近似值。 的第二近似值。
若 ,则 ,则 ;否则再过点( ;否则再过点( ), ( ), ( ),作弦,此弦与x轴交点的横坐标为 ),作弦,此弦与x轴交点的横坐标为

将 作为方程的根 作为方程的根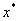 的第三近似值。 的第三近似值。
一般地,如果已求得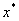 的近似值 的近似值 ,则过点( ,则过点( ), ( ), ( )作弦, 此弦与x轴交点的横坐标为 )作弦, 此弦与x轴交点的横坐标为
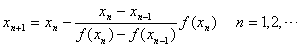 (8.8) (8.8)
将 作为方程的根 作为方程的根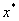 的第n+1个近似值。式(8.8)为双点弦法的迭代公式。 的第n+1个近似值。式(8.8)为双点弦法的迭代公式。
2.双点弦法的收敛性
定理8.3. 设 在区间[a,b]上存在二阶连续导数,且满足条件 在区间[a,b]上存在二阶连续导数,且满足条件
⑴  ; ;
⑵ 在[a,b]上不等于零 在[a,b]上不等于零
(3)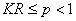 ,其中 ,其中
则以a,b为初始值, 由双点弦法的迭代公式(8.8)产生的近似根序列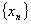 超线性收敛于 超线性收敛于
方程 在区间[a,b]内的惟一根 在区间[a,b]内的惟一根 。 。
证明 由条件(1)(2)知方程 在区间[a,b]内有唯一根 在区间[a,b]内有唯一根 。 。
因为

由线性插值余项得

其中 位于 位于 的最大值与最小值之间。 的最大值与最小值之间。
再由微分中值定理得

其中 位于 位于 之间, 之间,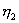 位于 位于 之间。 之间。
同理可得 的误差关系式 的误差关系式
 (8.9) (8.9)
其中 位于 位于 之间, 之间, 位于 位于 的最大值与最小值之间。 的最大值与最小值之间。
式(8.9)表示 的误差与 的误差与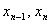 的误差之积成正比。 的误差之积成正比。
若令
 和 和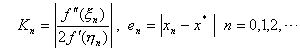
由条件(3)和式(8.9)得

于是有
即序列 收敛)根 收敛)根 。 。
设 具有p阶敛速,则由敛速定义知 具有p阶敛速,则由敛速定义知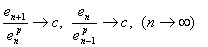
于是有
又由f(x)二阶导数连续和式(8.9)得
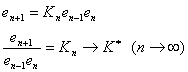
所以有
此式表明


即序列 具有敛速 具有敛速 ,也就是序列 ,也就是序列 超线性收敛于方程 超线性收敛于方程 在区间[a,b]内的惟一根 在区间[a,b]内的惟一根 。 。
例5 用双点弦法求方程 的最小正根。准确到 的最小正根。准确到
解: 因为 ,所以 ,所以 ,在区间[0,0.5]上, ,在区间[0,0.5]上,  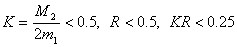
选取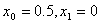 ,用双点弦法迭代公式 ,用双点弦法迭代公式

具体计算结果列表如下:
表8-5
n |
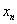
|

|
0 |
0.5 |
0.53125 |
1 |
0 |
-1 |
2 |
0.326530612 |
-0.016696065 |
3 |
0.332074957 |
2.63004072 |
4 |
0.331988974 |
-1.70108 |
5 |
0.331989029 |
-1.755 |
因为
所以
练习8.3
1. 用单点弦法求方程

的最小正根,准确到 . .
2.用双点弦法求方程
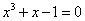
的最小正根,准确到 . .
练习题答案
1.
2.
|
|