设函数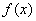 在区间[a,b]上连续,方程 在区间[a,b]上连续,方程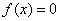 在区间[a,b]存在根 在区间[a,b]存在根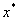 ,初值 ,初值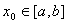 ,
将方程 ,
将方程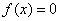 在区间[a,b]上同解变形为 在区间[a,b]上同解变形为
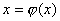 (8.10) (8.10)
如果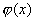 在[a,b]上连续,将初值 在[a,b]上连续,将初值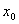 代入式(8.10)右端,计算得 代入式(8.10)右端,计算得
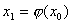
将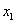 作为方程的根 作为方程的根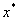 的第一近似值。 的第一近似值。
再将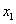 代入式(8.10)右端,计算得 代入式(8.10)右端,计算得
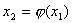
将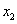 作为方程的根 作为方程的根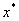 的第二近似值。 的第二近似值。
一般地,如果已计算出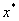 的第n个近似值 的第n个近似值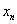 ,再将 ,再将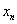 代入式(8.10)右端,计算得 代入式(8.10)右端,计算得
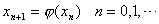 (8.11) (8.11)
将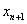 作为方程的根 作为方程的根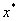 的第n+1个近似值。 的第n+1个近似值。
上述求方程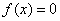 近似根方法称为一般迭代法,式(8.11)为一般迭代法的迭代公式, 近似根方法称为一般迭代法,式(8.11)为一般迭代法的迭代公式,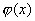 为一般迭代法的迭代函数。 为一般迭代法的迭代函数。
可以看出,建立一般迭代法的迭代公式的关键是方程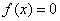 在区间[a,b]上的同解变形,在一般情况下,方程 在区间[a,b]上的同解变形,在一般情况下,方程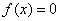 在区间[a,b]上会有多种形如式(8.10)的同解变形,因而也会有多种一般迭代法的迭代公式。下面看一个计算实例。 在区间[a,b]上会有多种形如式(8.10)的同解变形,因而也会有多种一般迭代法的迭代公式。下面看一个计算实例。
例6 试用几种不同的一般迭代法的迭代公式求方程
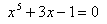
的正实根。
解 因为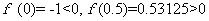 所以 所以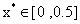
将方程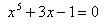
在区间[0 ,0.5]上同解变形
(1)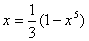 ,相应迭代公式为 ,相应迭代公式为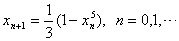
(2)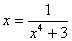 ,相应迭代公式为 ,相应迭代公式为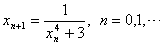
(3) ,相应迭代公式为 ,相应迭代公式为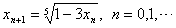
(4)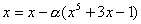 ,取 ,取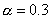 ,相应迭代公式为 ,相应迭代公式为
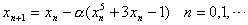
取初值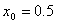 ,使用上面四种迭代公式具体计算如表: ,使用上面四种迭代公式具体计算如表:
表8-6
n |
公式(1)
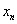
|
公式(2)
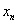
|
公式(3)
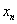
|
公式(4)
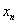
|
0 |
0.5 |
0. 5 |
0.5 |
0.5 |
1 |
0.32291666 |
0.326530612 |
-0.870550563 |
0.340625 |
2 |
0.332162942 |
0.332074957 |
1.292829258 |
0.335438137 |
3 |
0.331985504 |
0.331987642 |
-1.235471916 |
0.332269772 |
4 |
0.3319891 |
0.331989052 |
1.363132454 |
0.331946904 |
5 |
0.331989028 |
0.331989029 |
-1.253068331 |
0.331987056 |
这个计算结果表明,迭代公式(1),(2),(4)产生的序列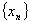 收敛,而迭代公式(3)产生的序列 收敛,而迭代公式(3)产生的序列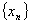 不收敛。 不收敛。
那么,迭代函数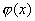 满足怎样的条件时,由迭代公式(8.11)产生的序列 满足怎样的条件时,由迭代公式(8.11)产生的序列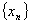 才收敛? 才收敛?
下面来讨论这一问题。
|