§2.5 波函数应满足的物理要求
波函数完全确定了一个物理体系的状态。因此，波函数除了满足薛定谔方程外，还必须满足某些物理要求。
首先，因为 
时刻粒子处于空间任意一点 
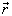处的几率密度都应该是惟一确定的，所以 
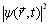必须是单值的。在保证了 
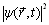是单值的情况下，
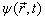的相因子 
没确定。如果
不是实常数，则两个差相因子
的波函数
和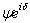 
导出的概率流密度将不同。因此，
必须是一个实常数。任意地指定
的整体相因子 
后，
也是单值的。
由于粒子在全空间出现的概率必为1，
应是平方可积的。
是有限连续的，而且在无限远处有足够好的收敛行为，这样的
自然满足这一物理要求。但这是充分条件，而不是必要条件。实际上，即使
有有限个孤立奇点，但相应的‘暇积分’存在, 仍可满足这一物理要求。
除了平方可积的波函数外，还必须用到一类非平方可积的归一为
函数的波函数，例如单色平面波。对这类波函数
当然不能再要求在无限远处有足够好的收敛行为了。
其次，概率流密度也是一个物理可测量，必须是单值﹑连续﹑有限的。
中含有
，
连续﹑单值且有限是
满足这一物理要求的充分条件，但不是必要条件。当
一些孤立点上不连续﹑不单值时，
却可能是单值﹑连续﹑有限的。例如，当
，尽管
不连续，却有
。
综上所述，只要满足薛定谔方程和以上物理要求的波函数就是可接受的。单值（确定到一个任意相因子）﹑有限﹑连续且在无限远处有足够好的收敛行为的波函数满足物理要求。但这仅是充分条件。更一般的， 可以有有限个孤立奇点，只要相应的‘暇积分’存在；
对非平方可积的波函数，也不再要求在无限远处有足够好的收敛行为；
可以不连续﹑不单值，只要保证
是单值﹑连续﹑有限的就可以了。
以一维情况为例，常见的波函数连接情况如下：
在势场连续有限処，
及
也连续有限。
在势场不连续处（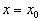 
），
,
有限，
及
也连续有限。但是，在一些特殊的情况下，粒子在不同的势能区域中具有不同的有效质量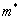 
，这时，就必须要求波函数的一阶导数与粒子有效质量之比是连续的。即，
（2.4.1）
。 （2.4.2）
（2.4.2）保证概率流是连续的。
当
无限或势场为
函数时，
连续，但
不连续。在求解一维问题时，上述这些情况的实例都会碰到。