§2.6 定态薛定谔方程
§2.6.1 定态薛定谔方程的建立
设体系的哈密顿算符中不显含时间 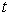 ,
,![]() 。这时可以用分离变量法求解薛定谔方程
。这时可以用分离变量法求解薛定谔方程
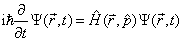 (2.6.1)
(2.6.1)
的特解。设
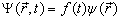 (2.6.2)
(2.6.2)
将上式代入(2.6.1)式,得
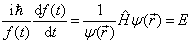 (2.6.3)
(2.6.3)
其中, 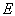 必是一个与
必是一个与 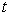 和
和 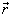 都无关的常数。于是有
都无关的常数。于是有
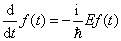 (2.6.4)
(2.6.4)
解之得
 (2.6.5)
(2.6.5)
因此,特解可改写成
 (2.6.6)
(2.6.6)
其中,
满足方程
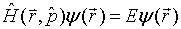 (2.6.7)
(2.6.7)
上式就是不含时间的薛定谔方程,称为定态薛定谔方程。
在量子力学中,若一个算符作用在一个波函数上,等于一个常数乘以该波函数,例如
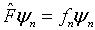 (2.6.8)
(2.6.8)
则称此方程为该算符的本征方程。并非任意常数都能满足这一方程,能够使这一方程有满足物理要求的解 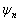 的常数
的常数 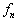 称为算符
称为算符  的第
个本征值。之所以加下指标n,是因为一般情况下这样的常数不是一个,而是很多个。波函数
称为相应于本征值
的第
个本征值。之所以加下指标n,是因为一般情况下这样的常数不是一个,而是很多个。波函数
称为相应于本征值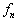 的本征函数。
的本征函数。