§2.4
几率密度与几率流密度
设 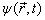 已归一化,粒子在
已归一化,粒子在![]() 时刻出现在
时刻出现在![]() 処的几率密度为
処的几率密度为
![]()
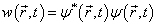 。
(2.4.1)
。
(2.4.1)
将两端对时间 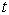 求偏微商,得到
求偏微商,得到
 。 (2.4.2)
。 (2.4.2)
若位势满足
,则薛定谔方程及其复共轭方程可以分别改写成如下形式
 (2.4.3)
(2.4.3)
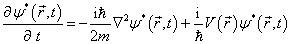 (2.4.4)
(2.4.4)
将(2.4.3)-(2.4.4)代入(2.4.2)式,得到
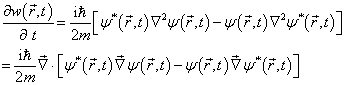
(2.4.5)
定义矢量
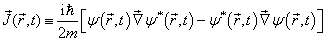 (2.4.6)
(2.4.6)
为几率流密度。由(2.4.6)可见,实波函数的几率流密度为零。
 (2.4.7)
(2.4.7)
此即概率守恒的微分表达式。它与流体力学中的连续性方程相同。
在空间任意有限的体积 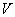 中将上式对坐标变量作积分
中将上式对坐标变量作积分
 , (2.4.8)
, (2.4.8)
利用高斯(Gauss)定理,得到几率守恒的积分表达式。
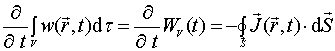 , (2.4.9)
, (2.4.9)
式中, 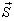 表示包围体积
表示包围体积 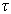 的封闭曲面,外法线规定为封闭曲面的正向,
的封闭曲面,外法线规定为封闭曲面的正向,![]() 是体积
是体积![]() 内的总概率。(2.4.9)式的物理意义是,单位时间内,粒子在体积
内的总概率。(2.4.9)式的物理意义是,单位时间内,粒子在体积![]() 中的总几率的增量等于单位时间内通过体积
中的总几率的增量等于单位时间内通过体积
![]() 的封闭曲面
的封闭曲面 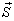 流入体积
流入体积![]() 中的几率。
中的几率。
将体积
![]() 扩展到全空间时,就不存在穿过体积
扩展到全空间时,就不存在穿过体积![]() 封闭面的概率流了,即此时
封闭面的概率流了,即此时![]() 。于是
。于是
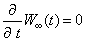 (2.4.10)
(2.4.10)
 。
(2.4.11)
。
(2.4.11)