§2.3.2
算符化规则
在量子力学中，波函数完全确定了体系的状态。但波函数并未直接给出物理量。为了得出体系的某一个物理量，就必须用相应的算符作用于这一体系的波函数才可。
在引入薛定谔方程的过程中，有两点应该注意到：一是经典物理学中的力学量已用算符来代替；二是上述的替代关系是一一对应的。此即所谓的算符化规则。按着惯例，一个力学量
对应的算符用
来表示。
基本的算符化规则可以表述为：
1.
用算符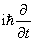
代替经典物理中的能量
，即
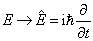（2.3.9）
2．用算符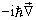 
代替经典物理中的动量 
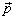，即
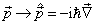（2.3.10）
显然，由此派生出来的经典动能
与算符的对应关系为
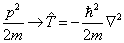（2.3.11）
哈密顿（Hamilton）量对应的算符为
（2.3.12）
于是，薛定谔方程可以简写成
（2.3.13）
上面提到的
、
与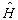 
分别称为动量算符、动能算符和哈密顿算符。
需要特别指出的是：
（1）、通常是在笛卡儿（Descartes）坐标系中使用算符化规则；
（2）、对于经典理论中的 项，应该将其用 替代后再使用算符化规则。