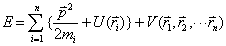， （2.3.7）
这里
是第
个单粒子的势能，
是n个粒子相互作用能。类比于（6）到（7）的过渡，可得多粒子体系波函数的方程
几点讨论：
（1）由（2.3.6），（2.3.8）可知，薛定谔方程是一个非相对论波动方程，只适用于低能粒子的体系。另一方面，这里没有讨论粒子的产生和消灭，因此方程只适合于粒子数不变的体系。
(2)薛定谔方程是一个复函数的方程，一般情况下，它的解（即波函数）应该也是一个时间和坐标的复函数。
(3)由于薛定谔方程中只含有描述状态的波函数对时间的一阶微商，所以，只要初始状态已知，那么，以后任意时刻
的状态
就确定了。可见，薛定谔方程给出了状态随时间变化的因果关系。
(4)薛定谔方程是线性微分方程，它的解
一定具有叠加性，而这正是状态叠加原理所要求的，反映出原理之间的一致性。