§2.3
薛定谔方程
§2.3.1
薛定谔方程的建立
经典物理学中，坐标和动量确定了体系的状态，因此就要有关于坐标和动量的运动方程，即牛顿方程。给定初始条件后，可完全确定体系以后的运动状态，即体系的坐标和动量。如前所述，波函数完全确定了一个量子体系的状态。如此，为了研究一个量子体系的状态及其变化，就必须有一个关于波函数的运动方程，以便给定初始条件和边界条件后，就能完全确定体系以后的波函数。没有任何原理能推出这种方程，这方程本身只能作为一个新的假设提出，因为微分方程包含的内容比它的某些解要多得多，所以即使知道了某些解，也不足以建立微分方程。但可尝试由一般的原则确定其形式，再由实验来检验。
1．
因为在任何时间，波函数都要满足叠加原理，所以方程必须是线性的。
2．
作为非相对论体系的方程，在伽利略变换下应是不变的。因此方程不应包含与运动状态有关的特征量，如动量﹑能量等。仅可以包含与运动状态无关的特征量，如﹑质量和电荷等。
3．
为了保证概率的正定性，方程应只是时间的一阶微分方程。如果方程是时间的二阶微分方程，则所定义的概率将依赖于
和
，这样，概率的正定性不能保证。根据数学物理方法中的史斗姆－刘维定理，二阶正规偏微分方程解的存在性和唯一性定理成立。所以方程对于坐标的微商也不应高于二阶。这样，给定初始和边界条件后，方程能唯一地确定以后的波函数。
4．
当
时，方程应给出经典力学的结果。
5．
对于有确定动量的自由粒子，方程的解应为单色平面波。
考虑到这些要求，可尝试确定方程。由条件4，对于经典自由粒子，有
，
（2.3.1）
由条件5和德布罗意关系，这时方程的解应为单色平面波
，
（2.3.2）
考虑到在直角坐标系中有
，
， （2.3.3）
由（2.3.1）－（2.3.3）可得
。 （2.3.4）
上式即为自由粒子满足的薛定谔方程。即使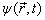
不是单色平面波，而是许多单色平面波的叠加，也容易证明上式是正确的。
若粒子在势场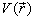
中运动，按照经典粒子的能量关系式
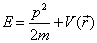（2.3.5）
类比自由粒子的情况，可以得到薛定谔波动方程：
（2.3.6）
对于多粒子体系，在经典力学中有