对于一个自由粒子波包
作傅立叶展开
，
（2.2.1）
。
（2.2.2）
在此展开式中，每一个分波都是有确定动量的平面单色波。每一个平面单色波都是粒子的一个可能的存在状态，
当然也是粒子可能的存在状态。实际上，任何一个粒子都不可能以一个单色波形式存在，它的概率波必是一个波包。另一方面，每次测得粒子的动量必是相应于某一个单色波的动量。这说明在量子理论中，波包必是由平面单色波叠加而成，即，在量子理论中，波叠加原理应成立。
量子理论中的叠加原理是：如果
、
、…
是体系的可能状态，则它们的线性叠加得出的波函数
， （2.2.3）
也是体系的一个可能状态。如果
是正交归一的，即，
， （2.2.4）
则在
态中，态
出现的概率是
。如果在态
中只能测得某物理量
的一个准确值
，
就是在态
中测得
的概率。这里
可以是有限的，无限的，也可以是连续的（这时，求和要化为积分）。
在上面的例子中，如果
是归一的，即
，则容易证明
。
实际上，由（2.2.1）－（2.2.2）有
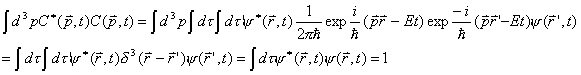
（2.2.5）
考虑到
， （2.2.6）
可知（4）中
是单色平面波
在态
中出现的概率幅，
是
时刻粒子在动量空间中
処出现的概率密度，即测得粒子动量为
的概率密度。
应强调指出，概率波的迭加只能是属于同一个粒子的﹑相应于不同状态的概率波的叠加，而不是不同粒子的概率波的叠加。而且，概率波的迭加是概率幅
相加，而不是概率相加。因此有干涉项出现，如双缝衍射干涉实验所表明那样。
量子理论中的态叠加不同于经典物理态叠加，起差别的主要原因是量子理论中的波是概率波。经典物理波的能量不仅与频率有关，而且与振幅有关。例如，同一个波的振幅加倍之后，在经典物理中这就是一个新的状态，而在量子理论中仍是原状态。又如，两个等振幅的平面单色波相加，在其为概率波或经典波的情况下，叠加后的状态显然是不同的。
概率波满足叠加原理，也就是一个体系的概率波对数乘和加法运算满足封闭性，如此，一个体系的所有波函数及零矢量形成一个线性空间。