一维
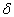 势为
势为
 (3.3.1)
(3.3.1)
.
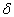 函数性质(见附录3)。
函数性质(见附录3)。![]() ,为势阱;
,为势阱;![]() ,为势垒。在
,为势垒。在
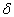 函数的诸多性质中,有一条需注意,就是
函数的诸多性质中,有一条需注意,就是
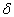 函数量纲。例如,由于
函数量纲。例如,由于
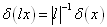 ,因此以坐标
,因此以坐标 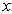 为自变量的
为自变量的 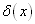 具有
具有  的量纲,(3.3.1)中的
的量纲,(3.3.1)中的![]() 应有(
应有(![]() )的量纲。质量为
)的量纲。质量为 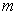 的粒子处于
的粒子处于
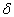 位势中所满足的定态薛定谔方程为
位势中所满足的定态薛定谔方程为
 (3.3.2)
(3.3.2)
 是上述方程的奇点,在
是上述方程的奇点,在  (
( 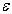 为一个小的正数)的邻域内,对上式作积分,得
为一个小的正数)的邻域内,对上式作积分,得
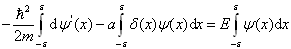 (3.3.3)
(3.3.3)
考虑到波函数连续性
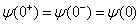 (3.3.4)
(3.3.4)
若令
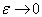 ,则由(3.3.3)得到在
,则由(3.3.3)得到在 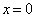 处波函数一阶导数的连接条件为
处波函数一阶导数的连接条件为
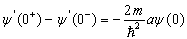 .
(3.3.5)
.
(3.3.5)
由上式可以清楚地看出,对于.
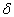 位势而言,除非
位势而言,除非 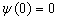 ,否则,函数的一阶导数是不连续的。
,否则,函数的一阶导数是不连续的。
在
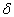 函数位阱中,质量为
函数位阱中,质量为 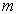 的粒子的定态薛定谔方程为
的粒子的定态薛定谔方程为
.
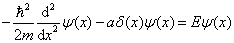 (3.3.6)
(3.3.6)
以.
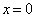 为界,将位势分为两个区,则两个区域内的定态薛定谔方程为
为界,将位势分为两个区,则两个区域内的定态薛定谔方程为