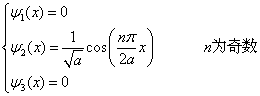（3.2.32）
上述波函数具有如下的特点，当坐标变量由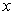 
变为 
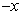时，若量子数 
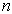为奇数，波函数不变，否则，波函数改变一个负号，通常把前者称为偶（正）宇称态，把后者称为奇（负）宇称态。这与定理4是一致的。
（2）、 
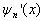的不连续性
在
処，微商是不连续的，例如，
。
但是，由于
是实波函数，概率流比为零，因此这解满足物理要求。
（3）、非对称势阱
若宽度为2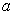 
的无限深方势阱的形式为非对称的，即
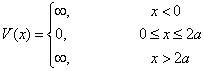（3.2.33）
平移坐标
,可求得能量本征值与相应的本征函数为
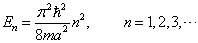（3.2.34）
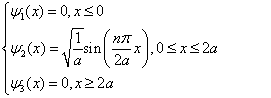（3.2.35）
由于该势能不具有空间反演对称性，波函数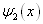 
中的自变量 
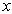只能在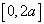 
区域内取值，故这时的波函数无确定的宇称。
（3）、与自由粒子的比较
由（3.2.12）式可知，随着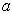 
的增大，能级的间距将逐渐变小，以致变成连续取值，也就是说，当势阱的宽度趋于无穷大时，该“自由粒子”就变成真正的自由粒子。